nLab topological quantum computation
Context
Computability
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Quantum systems
-
quantum algorithms:
Topological physics
Topological Physics – Phenomena in physics controlled by the topology (often: the homotopy theory) of the physical system.
General theory:
In metamaterials:
For quantum computation:
Contents
- Idea
- Related concepts
- References
- Need for topological protection
- Topological quantum computation with anyons
- Braid group representations (as topological quantum gates)
- Compilation to braid gate circuits
- Anyons in fractional quantum Hall systems
- Observation of anyons in fractional quantum Hall systems
- Superconducting defect anyons in FQH systems
- Anyons in topological superconductors
Idea
The idea of topological quantum computation is to implement quantum computation on quantum systems whose dynamics is described by topological quantum field theory (TQFT), so that the defining invariance of TQFTs under local perturbations implements protection of the quantum coherence by fundamental physical principles, instead of after the fact by quantum error correction.
General idea
The Problem of Contemporary Quantum Computing.
Common quantum computing architectures
(such as based on superconducting qbits, trapped ions, spin resonance, …)
suffer from an intrinsic tension:
-
quantum gates are implemented via interaction between subsystems,
-
but coherence requires avoiding interaction.
(cf. Waintal 2024, p3 or CCEHRSZ 07 p 272: “Quantum logic gates involving two atomic qubits must overcome the problem of the short range coherent interaction of neutral atoms, while maintaining atom confinement and suppressing decoherence. The main challenge is to perform the gate sufficiently fast compared to typical decoherence and relaxation times.”)
This problem haunts contemporary NISQ devices (cf. HHT 23),
whence the “Quantum Winter” (cf. McKenzie 24).
The bold idea of Topological Quantum Computing is to cut this Gordian knot:
Find quantum gates operating without interaction!
Can this work? In principle: Yes!
(By a phenomenon known as the “quantum adiabatic theorem”.)
For this we need a quantum system (say a crystalline quantum material)
with the following properties:
-
ground states degenracy:
even when completely frozen at absolute zero temperature
the system has more than one state to be in (even up to phase)
(Meaning: The Hilbert space of quantum states with energy eigenvalue is of dimension .)
-
an energy gap :
every excitation of the ground state has energy larger than
so that (light) quanta impacting the material have no interaction as long as they carry energy .
(Meaning: The material’s Hamiltonian has a spectral gap above the ground state.)
-
control parameters:
the above properties hold for a range of continuously tunable parameters
such as strain or voltage applied to the crystal
(Meaning: We have vector bundle of ground state Hilbert spaces over a topological space of parameter values .)
Adiabatic Transformation of Ground States.
Under these conditions:
-
after cooling such a system to its ground state,
-
sufficiently slow (“adiabatic”) variation of the external parameters
-
does not excite the system: it remains in a ground state
-
but the different ground states may transform into each other
(Meaning: Each parameter path induces a Berry phase unitary operator .)
This is part of a general phenomenon of quantum physics:
While quantum fluctuations are a little like thermal fluctuations
one key difference is that they remain present at absolute zero.
(Compare quantum phase transitions.)
Such operations on ground states are called holonomic quantum gates.
(From “holonomy” for the parallel transport of a Berry connection along loops.)
These are protected from external noise quanta of energy
but may still be sensitive no noise in the parameter paths.
Topological invariance.
To overcome this last issue, look for such quantum systems which in addition have:
-
parameter topology
The parameter space has “holes”, in that
some closed parameter paths cannot continuously be deformed to constant paths.
(Meaning: The fundamental group of parameter space is non-trivial.)
-
local parameter independence
All parameter paths with the same endpoints
that are continuous deformations of each other
yield the same transformation on ground states.
(Meaning: The Berry connection is flat.)
Quantum materials with all these properties are topologically ordered;
the resulting adiabatic quantum processes are topological quantum gates.
In principle, such topological quantum gates are:
-
protected against any noise in the parameter path.
In fact, the quantum operation induced by a parameter variation will
depend only on the discrete data of
how much the path winds around the holes of parameter space

This way,
topological quantum architecture may in principle
(be necessary to) solve the problem of quantum computing.
(cf. Sau 2017, Das Sarma 2022)
So far this is the theory behind topological quantum gates.
On the one hand it is extremely general:
- any kind of topologically parameterized quantum system could do.
On the other hand it is very ambitious:
- suitable such system have yet to be devised in the labs.
But the range of possibilities has hardly been explored,
most attention has been given to a single approach:
- braiding of anyonic defects in position space.
That’s what we discuss next.
Via anyon braiding
In specialization of the above general idea, the
original proposal due to Kitaev 2003 and FKLW 2003 (which has become canonized in the literature) is to envision
-
an effectively 2-dimensional quantum material (such as an atomic monolayer similar to graphene),
-
with some defect points of sorts (whose expected nature in real materials remains vague at this point),
-
whose positions constitute the above parameters, hence whose parameter space is a configuration space of points in the plane.
The motion in such a parameter space is a braid (of “worldlines” of defect points) and
if this acts non-trivially on the material’s ground states by adiabatic transformations,
then one refers to these defects as defect anyons:
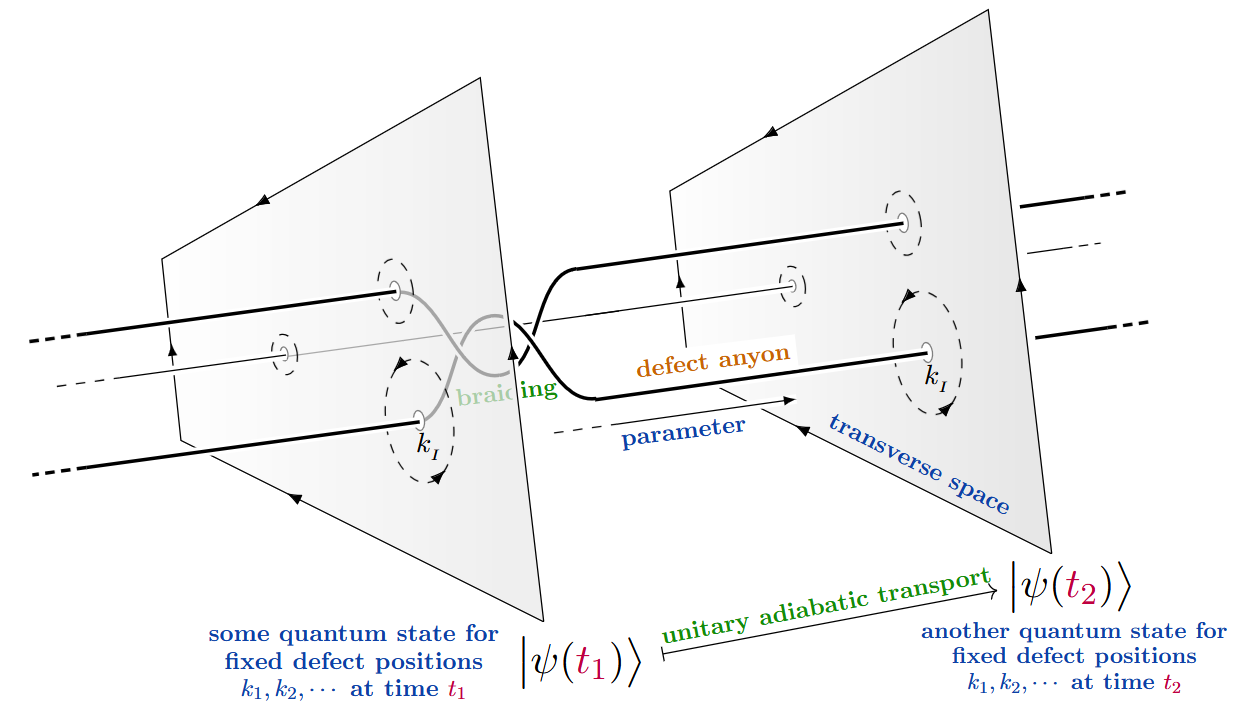
(graphics from SS24)
Status of anyonic quantum computation.
Experimentally,
at least abelian anyons
(whose braid representation factors through a representation of the symmetric group)
are seen in fractional quantum Hall systems,
though their controlled movement along the above lines seems out of reach.
Theoretically,
such defect anyons are expected to be effectively described by
some kind of Chern-Simons theory/Reshetikhin-Turaev theory
(and hence ultimately classified by modular tensor categories),
though attempts to derive some of these expectations from microscopic physics are rare.
(A more microscopic argument for anyonic defects not in position-space but in “reciprocal” momentum-space – the Brillouin torus –, appearing there as the familiar band nodes of topological semimetals, is made in SS23.)
The open problem of strongly-coupled quantum systems.
A general problem on both of these fronts is that
anyonic topological order is supposed to arise in strongly correlated systems which, like
all non-perturbative physics, remains ill-understood in general.
The directly analogous problem in particle physics,
where the the energy gap is known as the mass gap,
has been termed a Millennium Problem by the Clay Math Institute
(cf. the Mass Gap Problemap#ReferencesMassGapProblem))
One plausible approach on this front is to find
geometric engineering of anyonic topological order on M-branes
or their holographic dual bulk gravity.
Loosely related approaches.
Much attention in the 2010s had been given to claims of experimental detection of anyons in the form of “Majorana zero modes” (MZMs) – but these claims seem not to hold water. In any case, these MZMs are by design stuck at the end of nanowires and hence are not movable and in particular not braidable in the above sense.
More recently the idea of quantum simulation of anyons on ordinary quantum hardware has found more attention, though the relevance of this, if any, to the original idea of quantum-error protection by fundamental physical principles may remain to be discussed.
Topological quantum protocols.
Topological quantum computation protocols with defect anyons are often assumed to start by creating anyon/anti-anyon pairs out of the “anyon vacuum”, then braid their worldlines and finally annihilate them again — so that the total process is described by a link which, when regarded as a Wilson loop, may be understood as parameterizing a quantum observable of the Chern-Simons theory mentioned above:
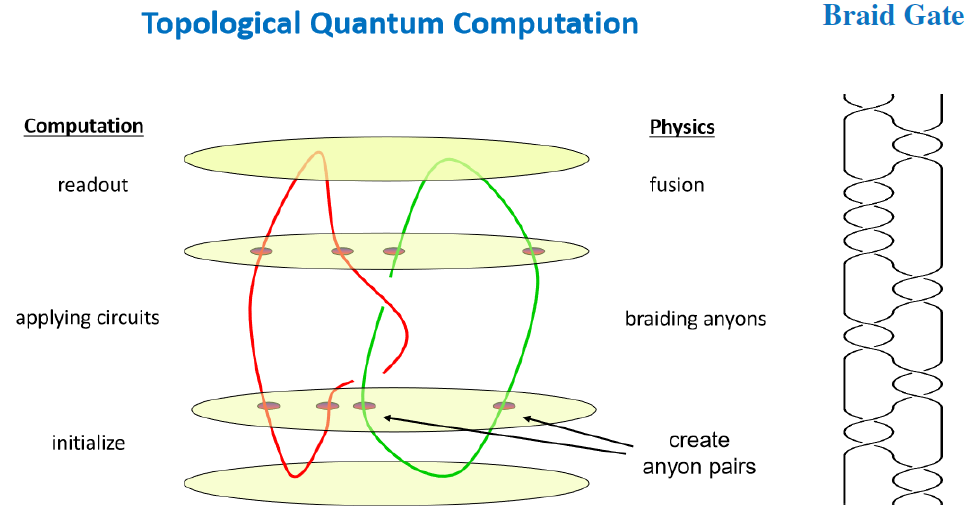
In any case, in this scheme the topological quantum gates are encoded by braid group-elements and are executed by actions through braid representations on the space of quantum states:

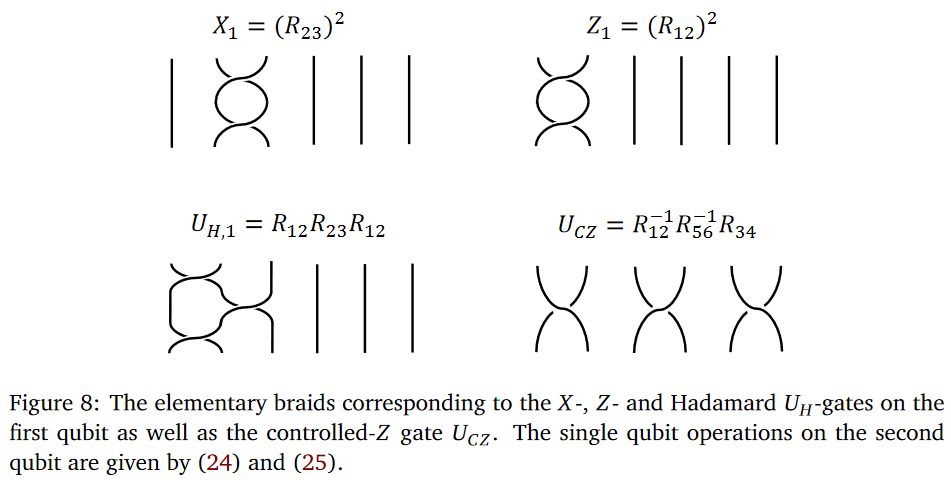
Topological Quantum Compilation.
This means that quantum gates based on anyon braiding are (going to be) quite different from the standard quantum gates traditionally considered in qbit-based quantum circuits.
For example, the following lengthy braid has been proposed [Hormozi, Zikos, Bonesteel & Simon (2007)] as a possible topological implementation of a single CNOT gate:
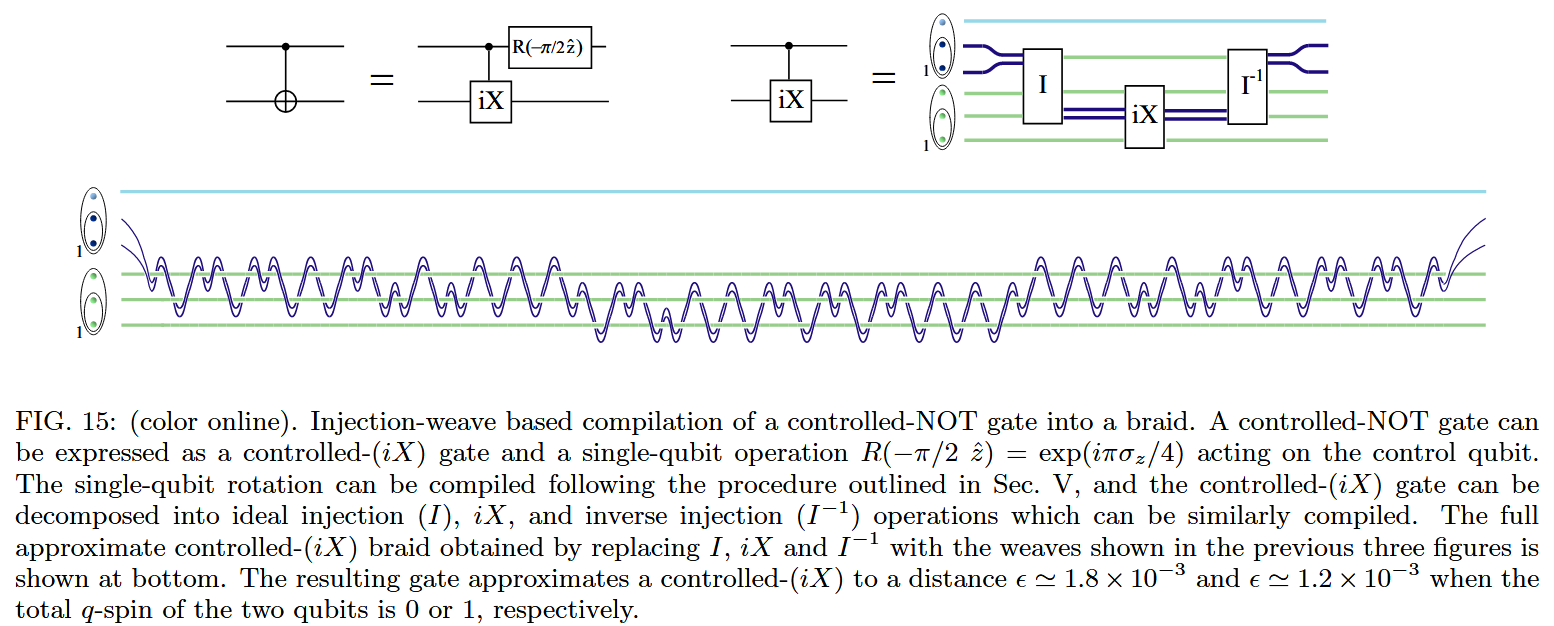
Hence if and when such topological quantum hardware becomes available, a major issue on the quantum software side will be the compilation of quantum algorithms to the exotic-seeming machine-level gates (cf. topological quantum compilation).
It has been argued that the complexity of this process will make its formal verification a practical necessity.
Extended TQC?
It may be interesting to note that:
-
(pure) braid group representations are equivalently degree-1 cocycles in the non-abelian cohomology of the configuration space of points (ordered) in the Euclidean plane,;
-
as such, braid representations are the first stage in a sequence that continues with weight systems on horizontal chord diagrams, these being the complex cohomology in higher degree of the configuration space of points (ordered) in Euclideam 3-space (see at weight systems are cohomology of loop space of configuration space):
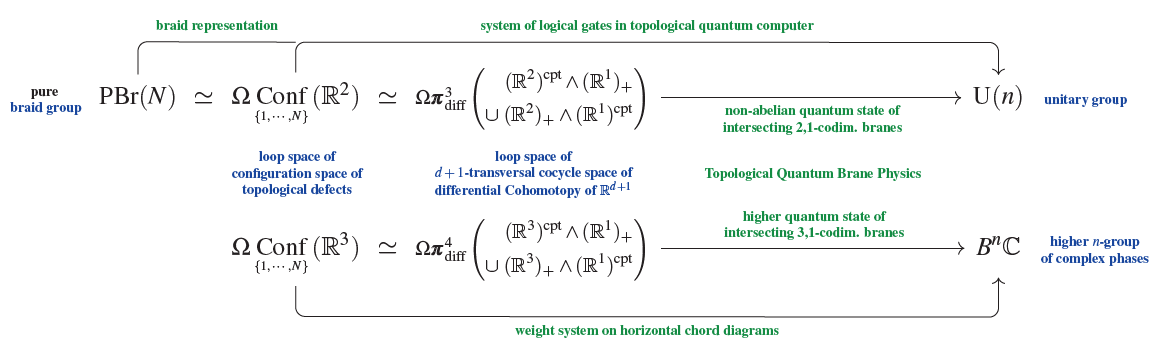
Here
-
is an Eilenberg-MacLane space/classifying space for the pure braid group
-
is a simply connected higher homotopy type:
This means that while every individual loop in is homotopically trivial (all “braid-gates” are equivalent) there is now non-trivial structure in higher-dimensional deformation families of braids (which is absent in ). Such structure would be reflected by extended TQFT.
Related concepts
References
Need for topological protection
Highlighting the need for topological stabilization mechanisms:
-
Freedman, Kitaev, Larsen & Wang 2003:
“the chief advantage of anyonic [topological quantum] computation would be physical error correction: An error rate scaling like , where is a length scale, and is some positive constant. In contrast, the “presumptive” qubit-model of quantum computation, which repairs errors combinatorically, requires a fantastically low initial error rate (about ) before computation can be stabilized. […] To reduce this model to engineering, very significant obstacles must be overcome: […] Although these challenges are daunting, they are, perhaps, less difficult than a head-on assault on the accuracy threshold in the quantum circuit model.
-
Jay Sau, A Roadmap for a Scalable Topological Quantum Computer, Physics 10 68 (2017)
“small machines are unlikely to uncover truly macroscopic quantum phenomena, which have no classical analogs. This will likely require a scalable approach to quantum computation. […] based on […] topological quantum computation (TQC) as envisioned by Alexei Kitaev and Michael Freedman […] The central idea of TQC is to encode qubits into states of topological phases of matter. Qubits encoded in such states are expected to be topologically protected, or robust, against the ‘prying eyes’ of the environment, which are believed to be the bane of conventional quantum computation.”
-
Sankar Das Sarma, Quantum computing has a hype problem, MIT Technology Review (March 2022)
“The qubit systems we have today are a tremendous scientific achievement, but they take us no closer to having a quantum computer that can solve a problem that anybody cares about. […] What is missing is the breakthrough […] bypassing quantum error correction by using far-more-stable qubits, in an approach called topological quantum computing.”
Topological quantum computation with anyons
The idea of topological quantum computation via a Chern-Simons theory with anyon braiding defects is due to:
-
Alexei Kitaev, Fault-tolerant quantum computation by anyons, Annals Phys. 303 (2003) 2-30 [doi:10.1016/S0003-4916(02)00018-0, arXiv:quant-ph/9707021]
-
Michael Freedman, P/NP, and the quantum field computer, Proc. Nat. Acad. Sci. 95 1 (1998) 98-101 [doi:10.1073/pnas.95.1.9]
-
Michael Freedman, Alexei Kitaev, Michael Larsen, Zhenghan Wang, Topological quantum computation, Bull. Amer. Math. Soc. 40 (2003), 31-38 [doi:10.1090/S0273-0979-02-00964-3, arXiv:quant-ph/0101025, pdf]
-
Michael Freedman, Michael Larsen, Zhenghan Wang, A modular functor which is universal for quantum computation, Communications in Mathematical Physics. 227 3 (2002) 605-622 [doi:10.1007/s002200200645, arXiv:quant-ph/0001108]
(specifically via su(2)-anyons)
-
Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, Sankar Das Sarma, Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80 1083 (2008) [doi:10.1103/RevModPhys.80.1083, arXiv:0707.1888]
-
Dmitry Melnikov, Andrei Mironov, Sergey Mironov, Alexei Morozov, Andrey Morozov: Towards topological quantum computer, Nucl. Phys. B926 (2018) 491-508 [doi:10.1016/j.nuclphysb.2017.11.016, arXiv:1703.00431]
(via R-matrix-solutions to the quantum Yang-Baxter equation)
and via a Dijkgraaf-Witten theory (like Chern-Simons theory but with discrete gauge group):
-
R. Walter Ogburn, John Preskill, Topological Quantum Computation, in: Quantum Computing and Quantum Communications, Lecture Notes in Computer Science 1509, Springer (1998) [doi:10.1007/3-540-49208-9_31]
-
Carlos Mochon, Anyons from non-solvable finite groups are sufficient for universal quantum computation, Phys. Rev. A 67 022315 (2003) [doi:10.1103/PhysRevA.67.022315, arXiv:quant-ph/0206128]
-
Carlos Mochon, Anyon computers with smaller groups, Phys. Rev. A 69 032306 (2004) [doi:10.1103/PhysRevA.69.032306, arXiv:quant-ph/0306063]
Proposals more specifically for topological quantum gates implemented in fractional quantum Hall systems:
-
D. V. Averin, V.J. Goldman: Quantum computation with quasiparticles of the fractional quantum Hall effect, Solid State Communications 121 1 (2001) 25-28 [doi:10.1016/S0038-1098(01)00447-1, arXiv:cond-mat/0110193]
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak: Topologically-Protected Qubits from a Possible Non-Abelian Fractional Quantum Hall State, Phys. Rev. Lett. 94 166802 (2005) [doi:10.1103/PhysRevLett.94.166802, arXiv:cond-mat/0412343]
-
Sergey Bravyi: Universal Quantum Computation with the Fractional Quantum Hall State, Phys. Rev. A 73 042313 (2006) [doi:10.1103/PhysRevA.73.042313, arXiv:quant-ph/0511178]
Monographs:
-
Zhenghan Wang, Topological Quantum Computation, CBMS Regional Conference Series in Mathematics 112, AMS 2010 (ISBN-13: 978-0-8218-4930-9, pdf)
-
Jiannis K. Pachos, Introduction to Topological Quantum Computation, Cambridge University Press (2012) [doi:10.1017/CBO9780511792908]
-
Tudor D. Stanescu, Part IV of: Introduction to Topological Quantum Matter & Quantum Computation, CRC Press 2020 (ISBN:9780367574116)
-
Steven H. Simon, Topological Quantum, Oxford University Press (2023) [ISBN:9780198886723, pdf, webpage]
Review:
-
Louis Kauffman, Quantum Topology and Quantum Computing, in: Samuel J. Lomonaco (ed.), Quantum Computation: A Grand Mathematical Challenge for the Twenty-First Century and the Millennium, Proceedings of Symposia in Applied Mathematics 58, AMS (2002) [pdf, doi:10.1090/psapm/058]
(in relation to quantum topology)
-
John Preskill: Topological Quantum Computation, Chapter 9 in: Quantum Computation, lecture notes (since 2004) [pdf, pdf]
-
Gavin K. Brennen, Jiannis K. Pachos, Why should anyone care about computing with anyons?, Proc. R. Soc. A 464 (2008) 1-24 [doi:10.1098/rspa.2007.0026, arXiv:0704.2241]
-
Ady Stern, Netanel H. Lindner: Topological Quantum Computation – From Basic Concepts to First Experiments, Science 339 6124 (2013) 1179-1184 [doi:10.1126/science.1231473, spire:2748124]
-
Eric C. Rowell, An Invitation to the Mathematics of Topological Quantum Computation, J. Phys.: Conf. Ser. 698 (2016) 012012 [doi:10.1088/1742-6596/698/1/012012, arXiv:1601.05288]
-
Ananda Roy, David P. DiVincenzo, Topological Quantum Computing, Lecture notes of the 48th IFF Spring School (2017) [arXiv:1701.05052]
-
Ville Lahtinen, Jiannis K. Pachos, A Short Introduction to Topological Quantum Computation, SciPost Phys. 3 021 (2017) [doi: 10.21468/SciPostPhys.3.3.021, arXiv:1705.04103]
-
Eric C. Rowell, Zhenghan Wang, Mathematics of Topological Quantum Computing, Bull. Amer. Math. Soc. 55 (2018), 183-238 (arXiv:1705.06206, doi:10.1090/bull/1605)
-
Bernard Field, Tapio Simula, Introduction to topological quantum computation with non-Abelian anyons, Quantum Science and Technology 3 (2018) 045004 [doi:10.1088/2058-9565/aacad2, arXiv:1802.06176]
-
Muhammad Ilyas, Quantum Field Theories, Topological Materials, and Topological Quantum Computing [arXiv:2208.09707]
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing [arXiv:2208.11762, spire:2141848]
-
Fabian Hassler: Topological quantum computing [arXiv:2410.13547]
-
Hisham Sati, Sachin Valera: Topological Quantum Computing, Encyclopedia of Mathematical Physics 2nd ed 4 (2025) 325-345 [doi:10.1016/B978-0-323-95703-8.00262-7]
-
Jason Alicea: What does it mean to create a topological qubit?, Quantum Frontiers blog (March 2025) [webpage]
Focus on abelian anyons:
-
Jiannis K. Pachos, Quantum computation with abelian anyons on the honeycomb lattice, International Journal of Quantum Information 4 6 (2006) 947-954 [doi:10.1142/S0219749906002328, arXiv:quant-ph/0511273]
-
James Robin Wootton, Dissecting Topological Quantum Computation, PhD thesis, Leeds (2010) [ethesis:1163, pdf, pdf]
“non-Abelian anyons are usually assumed to be better suited to the task. Here we challenge this view, demonstrating that Abelian anyon models have as much potential as some simple non-Abelian models. […] Though universal non-Abelian models are admittedly the holy grail of topological quantum computation, and rightly so, this thesis has shown that Abelian models are just as useful as non-universal non-Abelian models. […] Abelian models are a computationally powerful, fault-tolerant and experimentally realistic prospect for quantum computation.”
-
Seth Lloyd, Quantum computation with abelian anyons, Quantum Information Processing 1 1/2 (2002) [doi:10.1023/A:1019649101654, arXiv:quant-ph/0004010]
-
James R. Wootton, Jiannis K. Pachos: Universal Quantum Computation with Abelian Anyon Models, Electronic Notes in Theoretical Computer Science 270 2 (2011) 209-218 [doi:10.1016/j.entcs.2011.01.032, arXiv:0904.4373]
see also:
-
Menelaos Zikidis: Abelian Anyons and Fractional Quantum Hall Effect, Seminar notes (2017) [pdf, pdf]
-
Wade Bloomquist, Zhenghan Wang: On Topological Quantum Computing With Mapping Class Group Representations, J. Phys. A: Math. Theor. 52 (2019) 015301 [doi:10.1088/1751-8121/aaeea1, arXiv:1805.04622]
-
Yichen Hu, Biao Lian: Chiral Sachdev-Ye model: Integrability and chaos of anyons in , Phys. Rev. B 105 (2022) 125109 [doi:10.1103/PhysRevB.105.125109]
Realization in experiment (so far via quantum simulation of anyons on non-topological quantum hardware, cf. FF24, Fig 5, as in “topological codes” for quantum error correction):
on superconducting qbits:
- T. Andersen et al.: Non-Abelian braiding of graph vertices in a superconducting processor, Nature 618 (2023) 264–269 [arXiv:2210.10255, doi:10.1038/s41586-023-05954-4]
on trapped-ion quantum hardware:
-
Daniel Nigg, Markus Mueller, Esteban A. Martinez, Philipp Schindler, Markus Hennrich, Thomas Monz, Miguel A. Martin-Delgado, Rainer Blatt: Experimental Quantum Computations on a Topologically Encoded Qubit, Science 18 Jul 2014: Vol. 345, Issue 6194, pp. 302-305 (arXiv:1403.5426, doi:10.1126/science.1253742)
-
Mohsin Iqbal, Nathanan Tantivasadakarn: Topological Order from Measurements and Feed-Forward on a Trapped Ion Quantum Computer, Nature Communications Physics 7 (2024) 205 [doi:10.1038/s42005-024-01698-3, arXiv:2302.01917]
-
Mohsin Iqbal, Nathanan Tantivasadakarn, R. Verresen et al., Figure 5 in : Non-Abelian topological order and anyons on a trapped-ion processor, Nature 626 (2024) 505–511 [doi:10.1038/s41586-023-06934-4]
Nature research briefing: Topological matter created on a quantum chip produces quasiparticles with computing power [doi:10.1038/d41586-023-04126-8]
-
Michael Foss-Feig, Guido Pagano, Andrew C. Potter, Norman Y. Yao: Progress in Trapped-Ion Quantum Simulation, Annual Reviews of Condensed Matter Physics (2024) [arXiv:2409.02990 doi:10.1146/annurev-conmatphys-032822-045619]
Discussion of anyon braid gates via homotopy type theory:
-
David Jaz Myers, Hisham Sati, Urs Schreiber: Topological Quantum Gates in Homotopy Type Theory, Comm. Math. Phys. 405 172 (2024) [arXiv:2303.02382, doi:10.1007/s00220-024-05020-8]
-
David Jaz Myers: Topological Quantum Gates, talk at Running HoTT 2024, CQTS@NYUAD (April 2024) [video:kt]
Braid group representations (as topological quantum gates)
On linear representations of braid groups (see also at braid group statistics and interpretation as quantum gates in topological quantum computation):
- Ivan Marin, On the representation theory of braid groups, Annales mathématiques Blaise Pascal, 20 2 (2013) 193-260 (arXiv:math/0502118, dml:275607)
Review:
-
Chen Ning Yang, M. L. Ge (eds.). Braid Group, Knot Theory and Statistical Mechanics, Advanced Series in Mathematical Physics 9, World Scientific (1991) doi:10.1142/0796
(focus on quantum Yang-Baxter equation)
-
Camilo Arias Abad: Introduction to representations of braid groups, Rev. colomb. mat. 49 1 (2015) [doi:10.15446/recolma.v49n1.54160, arXiv:1404.0724]
-
Toshitake Kohno, Introduction to representation theory of braid groups, Peking 2018 (pdf, pdf)
in relation to modular tensor categories:
- Colleen Delaney, Lecture notes on modular tensor categories and braid group representations, 2019 (pdf, pdf)
Braid representations from the monodromy of the Knizhnik-Zamolodchikov connection on bundles of conformal blocks over configuration spaces of points:
-
Ivan Todorov, Ludmil Hadjiivanov, Monodromy Representations of the Braid Group, Phys. Atom. Nucl. 64 (2001) 2059-2068; Yad.Fiz. 64 (2001) 2149-2158 arXiv:hep-th/0012099, doi:10.1134/1.1432899
-
Ivan Marin, Sur les représentations de Krammer génériques, Annales de l’Institut Fourier, 57 6 (2007) 1883-1925 numdam:AIF_2007__57_6_1883_0
and understood in terms of anyon statistics:
- Xia Gu, Babak Haghighat, Yihua Liu, Ising- and Fibonacci-Anyons from KZ-equations, J. High Energ. Phys. 2022 15 (2022) [doi:10.1007/JHEP09(2022)015, arXiv:2112.07195]
Braid representations seen inside the topological K-theory of the braid group‘s classifying space:
-
Alejandro Adem, Daniel C. Cohen, Frederick R. Cohen, On representations and K-theory of the braid groups, Math. Ann. 326 (2003) 515-542 (arXiv:math/0110138, doi:10.1007/s00208-003-0435-8)
-
Frederick R. Cohen, Section 3 of: On braid groups, homotopy groups, and modular forms, in: J.M. Bryden (ed.), Advances in Topological Quantum Field Theory, Kluwer 2004, 275–288 (pdf)
See also:
- R. B. Zhang, Braid group representations arising from quantum supergroups with arbitrary and link polynomials, Journal of Mathematical Physics 33, 3918 (1992) (doi:10.1063/1.529840)
As quantum gates for topological quantum computation with anyons:
-
Louis H. Kauffman, Samuel J. Lomonaco, Braiding Operators are Universal Quantum Gates, New Journal of Physics 6 (2004) [doi:10.1088/1367-2630/6/1/134, arXiv:quant-ph/0401090]
(via R-matrix solutions to the quantum Yang-Baxter equation)
-
Yong Zhang, Louis H. Kauffman, Mo-Lin Ge: Yang–Baxterizations, Universal Quantum Gates and Hamiltonians, Quantum Inf Process 4 (2005) 159–197 [doi:10.1007/s11128-005-7655-7]
(via R-matrix solutions to the quantum Yang-Baxter equation)
-
Samuel J. Lomonaco, Louis Kauffman, Topological Quantum Computing and the Jones Polynomial, Proc. SPIE 6244, Quantum Information and Computation IV, 62440Z (2006) (arXiv:quant-ph/0605004)
(braid group representation serving as a topological quantum gate to compute the Jones polynomial)
-
Louis H. Kauffman, Samuel J. Lomonaco, Topological quantum computing and braid group representations, Proceedings Volume 6976, Quantum Information and Computation VI; 69760M (2008) (doi:10.1117/12.778068, rg:228451452)
-
C.-L. Ho, A. I. Solomon, C.-H. Oh: Quantum entanglement, unitary braid representation and Temperley-Lieb algebra, EPL 92 (2010) 30002 [doi:10.1209/0295-5075/92/30002, arXiv:1011.6229]
-
Rebecca Chen: Generalized Yang-Baxter Equations and Braiding Quantum Gates, Journal of Knot Theory and Its Ramifications 21 09 (2012) 1250087 [arXiv:1108.5215, doi:10.1142/S0218216512500873]
-
Louis H. Kauffman, Majorana Fermions and Representations of the Braid Group, International Journal of Modern Physics A 33 23 (2018) 1830023 [doi:10.1142/S0217751X18300235, arXiv:1710.04650]
-
David Lovitz, Universal Braiding Quantum Gates [arXiv:2304.00710]
Introduction and review:
-
Colleen Delaney, Eric C. Rowell, Zhenghan Wang, Local unitary representations of the braid group and their applications to quantum computing, Revista Colombiana de Matemáticas(2017), 50 (2):211 (arXiv:1604.06429, doi:10.15446/recolma.v50n2.62211)
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing arXiv:2208.11762
Realization of Fibonacci anyons on quasicrystal-states:
- Marcelo Amaral, David Chester, Fang Fang, Klee Irwin, Exploiting Anyonic Behavior of Quasicrystals for Topological Quantum Computing, Symmetry 14 9 (2022) 1780 arXiv:2207.08928, doi:10.3390/sym14091780
Realization on supersymmetric spin chains:
- Indrajit Jana, Filippo Montorsi, Pramod Padmanabhan, Diego Trancanelli, Topological Quantum Computation on Supersymmetric Spin Chains arXiv:2209.03822
See also:
- Yuanjie Ren, Peter Shor, Topological quantum computation assisted by phase transitions [arXiv:2311.00103]
Compilation to braid gate circuits
On approximating (cf. the Solovay-Kitaev theorem) given quantum gates by (i.e. compiling them to) cicuits of anyon braid gates (generally considered for su(2)-anyons and here mostly for universal Fibonacci anyons, to some extent also for non-universal Majorana anyons):
-
Nicholas E. Bonesteel, Layla Hormozi, Georgios Zikos, Steven H. Simon, Braid Topologies for Quantum Computation, Phys. Rev. Lett. 95 140503 (2005) [doi:10.1103/PhysRevLett.95.140503, arXiv:quant-ph/0505065]
-
Layla Hormozi, Georgios Zikos, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Compiling, Phys. Rev. B 75 165310 (2007) [doi:10.1103/PhysRevB.75.165310, arXiv:quant-ph/0610111]
-
Layla Hormozi, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Computing with Read-Rezayi States, Phys. Rev. Lett. 103 160501 (2009) [doi:10.1103/PhysRevLett.103.160501, arXiv:0903.2239]
-
M. Baraban, Nicholas E. Bonesteel, Steven H. Simon, Resources required for topological quantum factoring, Phys. Rev. A 81 062317 (2010) [doi:10.1103/PhysRevA.81.062317, arXiv:1002.0537]
(focus on compiling Shor's algorithm)
-
Vadym Kliuchnikov, Alex Bocharov, Krysta M. Svore, Asymptotically Optimal Topological Quantum Compiling, Phys. Rev. Lett. 112 140504 (2014) [doi:10.1103/PhysRevLett.112.140504, arXiv:1310.4150, talk recording: doi:10.48660/13100129]
-
Joren W. Brunekreef, Topological Quantum Computation and Quantum Compilation, Utrecht (2014) [hdl:20.500.12932/17738]
-
Yuan-Hang Zhang, Pei-Lin Zheng, Yi Zhang, Dong-Ling Deng, Topological Quantum Compiling with Reinforcement Learning, Phys. Rev. Lett. 125 170501 (2020) [doi:10.1103/PhysRevLett.125.170501, arXiv:2004.04743]
-
Emil Génetay-Johansen, Tapio Simula, Section IV of: Fibonacci anyons versus Majorana fermions – A Monte Carlo Approach to the Compilation of Braid Circuits in Anyon Models, PRX Quantum 2 010334 (2021) [doi:10.1103/PRXQuantum.2.010334, arXiv:2008.10790]
-
Cheng-Qian Xu, D. L. Zhou, Quantum teleportation using Ising anyons, Phys. Rev. A 106 012413 (2022) [doi:10.1103/PhysRevA.106.012413, arXiv:2201.11923]
(focus on implemening the quantum teleportation-protocol with Ising anyons)
Approximating all topological quantum gates by just the weaves among all braids:
-
Steven H. Simon, Nick E. Bonesteel, Michael H. Freedman, N. Petrovic, Layla Hormozi, Topological Quantum Computing with Only One Mobile Quasiparticle, Phys. Rev. Lett. 96 (2006) 070503 (arXiv:quant-ph/0509175, doi:10.1103/PhysRevLett.96.070503)
-
Layla Hormozi, Georgios Zikos, Nick E. Bonesteel, Steven H. Simon, Topological quantum compiling, Phys. Rev. B 75, 165310 (doi:10.1103/PhysRevB.75.165310, arXiv:quant-ph/0610111)
-
Mohamed Taha Rouabah, Compiling single-qubit braiding gate for Fibonacci anyons topological quantum computation (arXiv:2008.03542)
Anyons in fractional quantum Hall systems
References on anyon-excitations (satisfying braid group statistics) in the quantum Hall effect (for more on the application to topological quantum computation see the references there):
The prediction of abelian anyon-excitations in the quantum Hall effect (i.e. satisfying braid group statistics in 1-dimensional linear representations of the braid group) by computation of Berry phases of Laughlin wavefunctions via the quantum adiabatic theorem:
-
Bertrand I. Halperin: Statistics of Quasiparticles and the Hierarchy of Fractional Quantized Hall States, Phys. Rev. Lett. 52 (1984) 1583 [doi:10.1103/PhysRevLett.52.1583]
Erratum, Phys. Rev. Lett. 52 (1984) 2390 [doi:10.1103/PhysRevLett.52.2390.4]
-
Daniel P. Arovas, John Robert Schrieffer, Frank Wilczek, Fractional Statistics and the Quantum Hall Effect, Phys. Rev. Lett. 53 (1984) 722 [doi:10.1103/PhysRevLett.53.722]
(for filling fraction )
-
W. P. Su: Statistics of the fractionally charged excitations in the quantum Hall effect, Phys. Rev. B 34 (1986) 1031 [doi:10.1103/PhysRevB.34.1031]
(claim for general filling fraction )
-
A. S. Goldhaber, Jainendra K. Jain: Characterization of fractional-quantum-Hall-effect quasiparticles, Physics Letters A 199 3–4 (1995) 267-273 [doi:10.1016/0375-9601(95)00101-8, arXiv:cond-mat/9501080]
(for Jain series fractions )
-
(review)
The original discussion of non-abelian anyon-excitations in the quantum Hall effect (i.e. satisfying braid group statistics in higher dimensional linear representations of the braid group, related to modular tensor categories):
- Gregory Moore, Nicholas Read, Nonabelions in the fractional quantum Hall effect, Nucl. Phys. 360B(1991)362 (pdf, doi:10.1016/0550-3213(91)90407-O)
Review:
-
Ady Stern, Anyons and the quantum Hall effect – A pedagogical review, Annals of Physics 323 1 (2008) 204-249 [doi:10.1016/j.aop.2007.10.008, arXiv:0711.4697]
-
Menelaos Zikidis: Abelian Anyons and Fractional Quantum Hall Effect, Seminar notes (2017) [pdf, pdf]
-
Ady Stern: Engineering Non-Abelian Quasi-Particles in Fractional Quantum Hall States – A Pedagogical Introduction, Ch. 9 in: Fractional Quantum Hall Effects, World Scientific (2020) 435-486 [doi:10.1142/9789811217494_0009]
-
D. E. Feldman, Bertrand Halperin: Fractional charge and fractional statistics in the quantum Hall effects, Rep. Prog. Phys. 84 (2021) 076501 [doi:10.1088/1361-6633/ac03aa, arXiv:2102.08998]
On (anyons in) fractional quantum Hall systems as potential quantum hardware for topological quantum computing:
-
D. V. Averin, V. J. Goldman: Quantum computation with quasiparticles of the fractional quantum Hall effect, Solid State Communications 121 1 (2001) 25-28 [doi:10.1016/S0038-1098(01)00447-1, arXiv:cond-mat/0110193]
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak: Topologically-Protected Qubits from a Possible Non-Abelian Fractional Quantum Hall State, Phys. Rev. Lett. 94 166802 (2005) [doi:10.1103/PhysRevLett.94.166802, arXiv:cond-mat/0412343]
-
Sergey Bravyi: Universal Quantum Computation with the Fractional Quantum Hall State, Phys. Rev. A 73 042313 (2006) [doi:10.1103/PhysRevA.73.042313, arXiv:quant-ph/0511178]
-
Maissam Barkeshli, Xiao-Liang Qi: Synthetic Topological Qubits in Conventional Bilayer Quantum Hall Systems, Phys. Rev. X 4 (2014) 041035 [doi:10.1103/PhysRevX.4.041035, arXiv:1302.2673]
-
Roger S. K. Mong et al.: Universal Topological Quantum Computation from a Superconductor-Abelian Quantum Hall Heterostructure, Phys. Rev. X 4 (2014) 011036 [doi:10.1103/PhysRevX.4.011036, arXiv:1307.4403]
Observation of anyons in fractional quantum Hall systems
While the occurrence of anyon-excitations in the fractional quantum Hall effect is a robust theoretical prediction (see the references above), and while the fractional quantum Hall effect itself has long been established in experiment, the actual observation of anyons in these systems is subtle.
An early claim of the observation of non-abelian anyons seems to remain unconfirmed:
- Sanghun An, P. Jiang, H. Choi, W. Kang, S. H. Simon, L. N. Pfeiffer, K. W. West, K. W. Baldwin, Braiding of Abelian and Non-Abelian Anyons in the Fractional Quantum Hall Effect [arXiv:1112.3400]
Observation in gallium arsenide () semiconductor heterostructures:
-
H. Bartolomei, et al.: Fractional statistics in anyon collisions, Science 368 6487 (2020) 173-177 [doi:10.1126/science.aaz5601, arXiv:2006.13157]
-
James Nakamura et al.: Aharonov–Bohm interference of fractional quantum Hall edge modes, Nature Physics 15 563–569 (2019) [doi:10.1038/s41567-019-0441-8, arXiv:1901.08452]
-
James Nakamura et al.: Direct observation of anyonic braiding statistics, Nat. Phys. 16 (2020) 931–936 [doi:10.1038/s41567-020-1019-1, arXiv:2006.14115]
-
Bob Yirka, Best evidence yet for existence of anyons, PhysOrg News (July 10, 2020) [phys.org/news/2020-07]
-
Davide Castelvecchi: Welcome anyons! Physicists find best evidence yet for long-sought 2D structures, Nature News, 583 (03 July 2020) 176-177 [doi:10.1038/d41586-020-01988-0]
-
James Nakamura et al.: Impact of bulk-edge coupling on observation of anyonic braiding statistics in quantum Hall interferometers, Nature Communications 13 344 (2022) [doi:10.1038/s41467-022-27958-w, arXiv:2107.02136]
-
James Nakamura et al.: Fabry-Perot interferometry at the fractional quantum Hall state, Phys. Rev. X 13 (2023) 041012 [doi:10.1103/PhysRevX.13.041012, arXiv:2304.12415]
-
M. Ruelle et al.: Comparing fractional quantum Hall Laughlin and Jain topological orders with the anyon collider, Physical Review X 13 (2023) 011031 [doi:10.1103/PhysRevX.13.011031, arXiv:2210.01066]
-
Pierre Glidic et al: Cross-Correlation Investigation of Anyon Statistics in the and Fractional Quantum Hall States, Phys. Rev. X 13 011030 (2023) [doi:10.1103/PhysRevX.13.011030, arXiv:2210.01054]
-
Pierre Glidic et al.: Signature of anyonic statistics in the integer quantum Hall regime, Nature Commun. 15 6578 (2024) 1 [doi:10.1038/s41467-024-50820-0, arXiv:2401.06069]
-
Hemanta Kumar Kundu et al.: Anyonic interference and braiding phase in a Mach-Zehnder interferometer, Nature Physics 19 (2023) 515–521 [doi:10.1038/s41567-022-01899-z, arXiv:2203.0420]
-
A. Veillon et al.: Observation of the scaling dimension of fractional quantum Hall anyons, Nature 632 (2024) 517–521 [doi:10.1038/s41586-024-07727-z]
-
Bikash Ghosh, Maria Labendik, Liliia Musina, Vladimir Umansky, Moty Heiblum, David F. Mross: Anyonic Braiding in a Chiral Mach-Zehnder Interferometer, Nature Physics (2025) [doi:10.1038/s41567-025-02960-3, arXiv:2410.16488]
and in graphene heterostructures:
-
Noah Samuelson et al.: Anyonic statistics and slow quasiparticle dynamics in a graphene fractional quantum Hall interferometer [arXiv:2403.19628]
-
Jehyun Kim et al.: Aharonov-Bohm Interference in Even-Denominator Fractional Quantum Hall States [arXiv:2412.19886]
See also:
- Flavio Ronetti et al.: Probing anyon statistics on a single-edge loop in the fractional quantum Hall regime [arXiv:2506.09774]
On appatent bound states of FQH anyons:
- Mytraya Gattu, Jainendra K. Jain: Molecular anyons in fractional quantum Hall effect [arXiv:2505.22782]
Superconducting defect anyons in FQH systems
On non-abelian (parafermionic Majorana zero mode) defect anyons associated with superconducting islands inside abelian fractional quantum Hall systems:
-
Netanel H. Lindner, Erez Berg, Gil Refael, Ady Stern: Fractionalizing Majorana fermions: non-abelian statistics on the edges of abelian quantum Hall states, Phys. Rev. X 2 (2012) 041002 [doi:10.1103/PhysRevX.2.041002arXiv:1204.5733]
-
David J. Clarke, Jason Alicea, Kirill Shtengel: Exotic non-Abelian anyons from conventional fractional quantum Hall states, Nature Communications 4 1348 (2013) [ncomms:2340, arXiv:1204.5479]
-
Abolhassan Vaezi: Fractional topological superconductor with fractionalized Majorana fermions, Phys. Rev. B 87 (2013) 035132 [doi:10.1103/PhysRevB.87.035132, arXiv:1204.6245]
-
Roger S. K. Mong, David J. Clarke, Jason Alicea, Netanel H. Lindner, Paul Fendley, Chetan Nayak, Yuval Oreg, Ady Stern, Erez Berg, Kirill Shtengel, Matthew P. A. Fisher: Universal Topological Quantum Computation from a Superconductor-Abelian Quantum Hall Heterostructure, Phys. Rev. X 4 (2014) 011036 [doi:10.1103/PhysRevX.4.011036, arXiv:1307.4403]
-
Younghyun Kim, David J. Clarke, Roman M. Lutchyn: Coulomb Blockade in Fractional Topological Superconductors, Phys. Rev. B 96 (2017) 041123 [doi:10.1103/PhysRevB.96.041123, arXiv:1703.00498]
-
Luiz H. Santos, Taylor L. Hughes: Parafermionic Wires at the Interface of Chiral Topological States, Phys. Rev. Lett. 118 (2019) 136801 [doi:10.1103/PhysRevLett.118.136801]
-
Luiz H. Santos: Parafermions in Hierarchical Fractional Quantum Hall States, Phys. Rev. Research 2 (2020) 013232 [doi:10.1103/PhysRevResearch.2.013232, arXiv:1906.07188]
Anyons in topological superconductors
On anyon-excitations in topological superconductors.
via Majorana zero modes:
Original proposal:
- Nicholas Read, Dmitry Green, Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries, and the fractional quantum Hall effect, Phys. Rev. B61:10267, 2000 (arXiv:cond-mat/9906453)
Review:
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak, Majorana Zero Modes and Topological Quantum Computation, npj Quantum Information 1, 15001 (2015) (nature:npjqi20151)
-
Nur R. Ayukaryana, Mohammad H. Fauzi, Eddwi H. Hasdeo, The quest and hope of Majorana zero modes in topological superconductor for fault-tolerant quantum computing: an introductory overview (arXiv:2009.07764)
-
Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors [arXiv:2301.11614]
Further developments:
-
Meng Cheng, Victor Galitski, Sankar Das Sarma, Non-adiabatic Effects in the Braiding of Non-Abelian Anyons in Topological Superconductors, Phys. Rev. B 84, 104529 (2011) (arXiv:1106.2549)
-
Javad Shabani et al., Two-dimensional epitaxial superconductor-semiconductor heterostructures: A platform for topological superconducting networks, Phys. Rev. B 93 155402 (2016) [doi:10.1103/PhysRevB.93.155402, arXiv:1511.01127]
-
Javad Shabani et al., Zero-Energy Modes from Coalescing Andreev States in a Two-Dimensional Semiconductor-Superconductor Hybrid Platform, Phys. Rev. Lett. 119 (2017) 176805 [doi:10.1103/PhysRevLett.119.176805, arXiv:1703.03699]
-
Javad Shabani et al., Fusion of Majorana Bound States with Mini-Gate Control in Two-Dimensional Systems, Nature Communications 13 (2022) 1738-1747 [doi:10.1038/s41467-022-29463-6, arXiv:2101.09272]
-
Javad Shabani et al., Quasiparticle dynamics in epitaxial Al-InAs planar Josephson junctions, PRX Quantum 4 030339 (2023) [doi:10.1103/PRXQuantum.4.030339, arXiv:2303.04784]
-
William F. Schiela, Peng Yu, Javad Shabani: Progress in superconductor-semiconductor topological Josephson junctions, PRX Quantum 5 (2024) 030102 [doi:10.1103/PRXQuantum.5.030102, arXiv:2408.12749]
via Majorana zero modes restricted to edges of topological insulators:
- Biao Lian, Xiao-Qi Sun, Abolhassan Vaezi, Xiao-Liang Qi, Shou-Cheng Zhang: Topological quantum computation based on chiral Majorana fermions, PNA 115 43 (2018) 10938-10942 [doi:10.1073/pnas.1810003115]
Concerning measurement-based quantum gates on Majorana zero modes:
- Torsten Karzig, Yuval Oreg, Gil Refael, Michael H. Freedman: Robust Majorana magic gates via measurements, Phys. Rev. B 99 (2019) 144521 [doi:10.1103/PhysRevB.99.144521, arXiv:1812.10498]
See also:
- Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors arXiv:2301.11614
Last revised on February 22, 2025 at 19:25:23. See the history of this page for a list of all contributions to it.