nLab 't Hooft double line notation
Context
Lie theory
∞-Lie theory (higher geometry)
Background
Smooth structure
Higher groupoids
Lie theory
∞-Lie groupoids
∞-Lie algebroids
Formal Lie groupoids
Cohomology
Homotopy
Related topics
Examples
-Lie groupoids
-Lie groups
-Lie algebroids
-Lie algebras
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
Double line notation
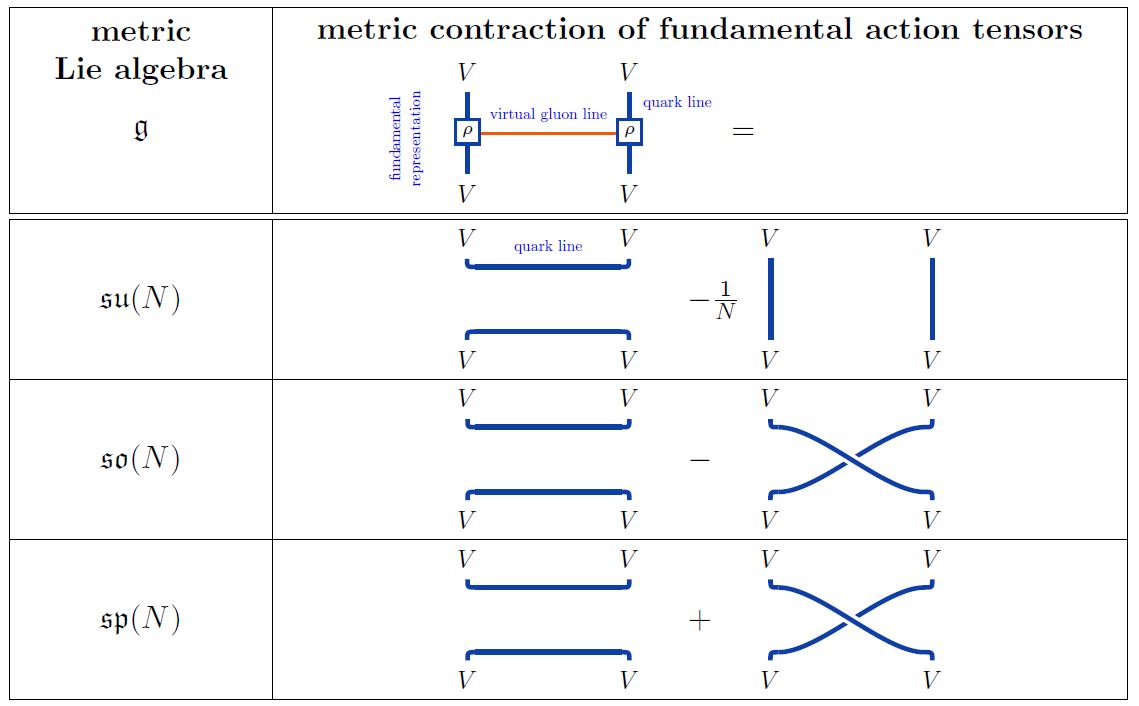
What is called ’t Hooft double line notation (following ’t Hooft 74) is the observation that for the fundamental representations of semisimple Lie algebras . the Lie algebra weight of a -Yang-Mills theory Feynman diagram with internal/virtual gluon lines is equivalent to one without any virtual gluon-lines, obtained by:
1) using the Jacobi identity to replace all internal gluon vertices by (linear combinations of) quark-gluon vertices

2) replacing any remaining internal gluon line together with the quark interaction vertices at its ends (equivalently: an M2-brane 3-algebra tensor) by (a linear combination of) double quark-lines, according to the following rules:
For example, for a special orthogonal Lie algebra, the ’t Hooft double line notation of a single trivalent vertex inside a single Wilson loop is the following:
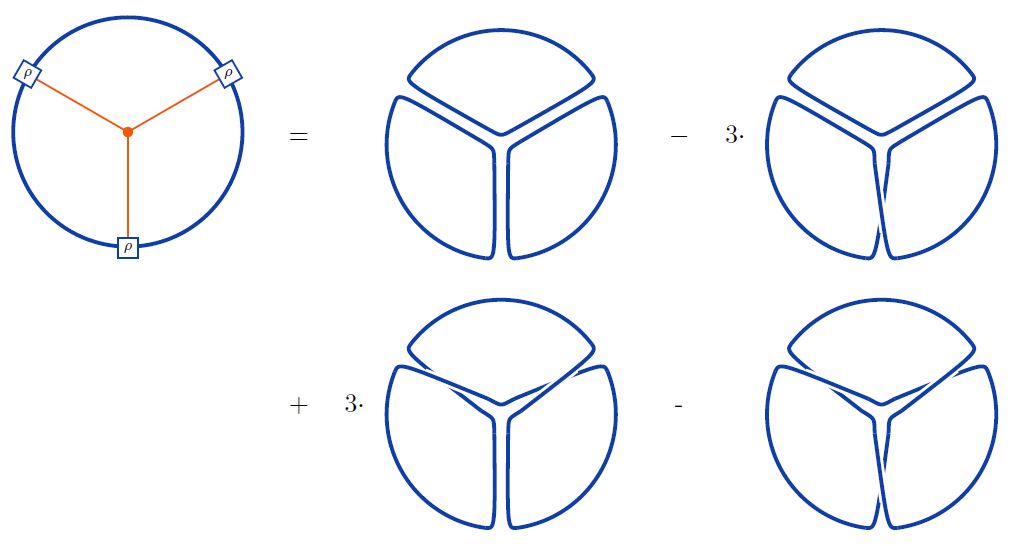
Here we are using the string diagram/Penrose notation from metric Lie representations.
graphics from Sati-Schreiber 19c
Attribution. In ’t Hooft 74 this is observed for the unitary Lie algebra (see also Bar-Natan 95 (34), Chmutov-Duzhin-Mostovoy 11, p. 177, in which case only the first summand of the expressions above appears. The generalization to arbitrary semisimple Lie algebras is observed in Cvitanović 76, Fig. 14, reviewed for su(N), so(N) and sp(N) in Cvitanović 08 (9.57), (10.13) and (12.9) and for so(N) in Chmutov-Duzhin-Mostovoy 11, 6.2.6. For the case see also Bar-Natan 95, Section 6.3 (with an eye towards Vassiliev knot invariants) and Cicuta 82, Ita-Nieder-Oz 02, Figure 3, McGreevy-Swingle 08, Figure 10 (with more discussion of the large N limit). The case of gl(N) is considered in Bar-Natan 96, Section 2.2, Chmutov-Duzhin-Mostovoy 11, 6.2.5, and the case sl(N) in Chmutov-Duzhin-Mostovoy 11, 6.1.8, Jackson-Moffat 19, Section 14.4.
Surface notation
Furthermore, one may regard the resulting double-line diagrams as a ribbon graph thickening of the original Feynman diagrams, and thus as surfaces with boundary and with markings on the boundary.
In the case this means that a single virtual gluon line is represented by the formal linear combination of a strip (marked disk) and a twisted strip:
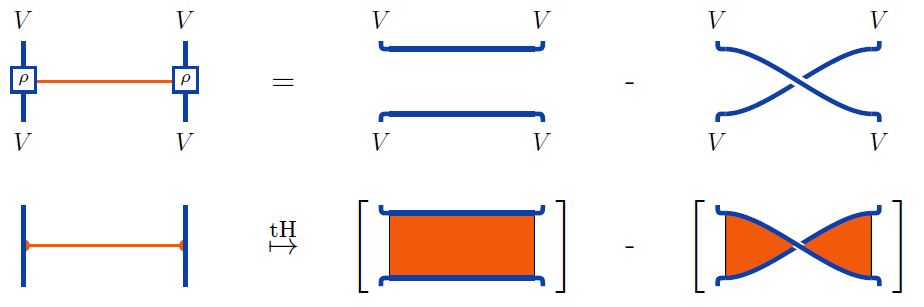
Using this on the reduction of internal gluon vertices by the Jacobi identity as above one finds that a single gluon vertex turns into the following linear combination of marked surfaces:
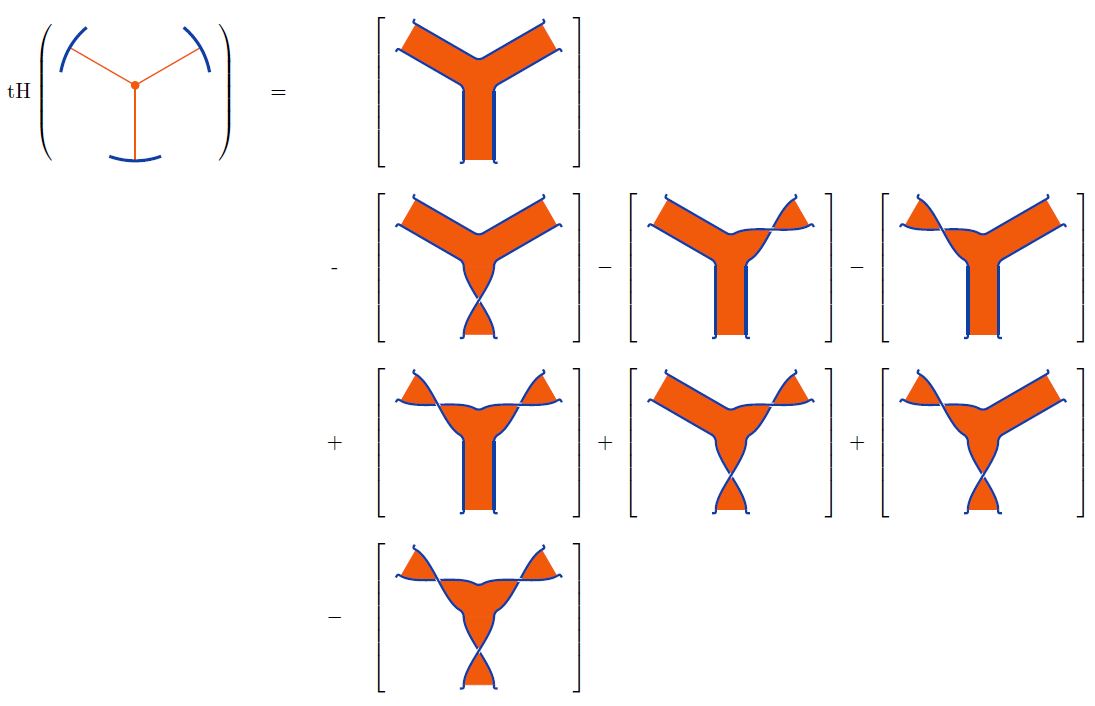
For example:

graphics from Sati-Schreiber 19c
This gives open string worldsheets. Regarding them as such in the case of Chern-Simons theory exhibits Chern-Simons theory as an open topological string theory (Witten 92, see Figures 1 & 2) even for small N.
For AdS/CFT duality relating super Yang-Mills theory to closed string theory and open to closed topological string theory (Gopakumar-Vafa 98) there is an operation of gluing in faces to turn these open strings into closed string worldsheets, see Gaiotto-Rastelli 03, Section 1.1 and see Marino 04, Section III, p. 14 for a clear statement).
Here open/closed string duality plays a subtle role in interpreting the 't Hooft double line notation of gauge theory Feynman diagrams in the large N limit alternatively as open string or as closed string worldsheets, see also Gopakumar 04.
As a surface-valued weight system
After averaging over the permutations of the ordering of the external vertices (those on the Wilson line) of a Jacobi diagram, this construction respects the STU relation on Jacobi diagrams and hence gives a weight system with values in marked surfaces (Bar-Natan 95, Theorem 10 with Theorem 8):
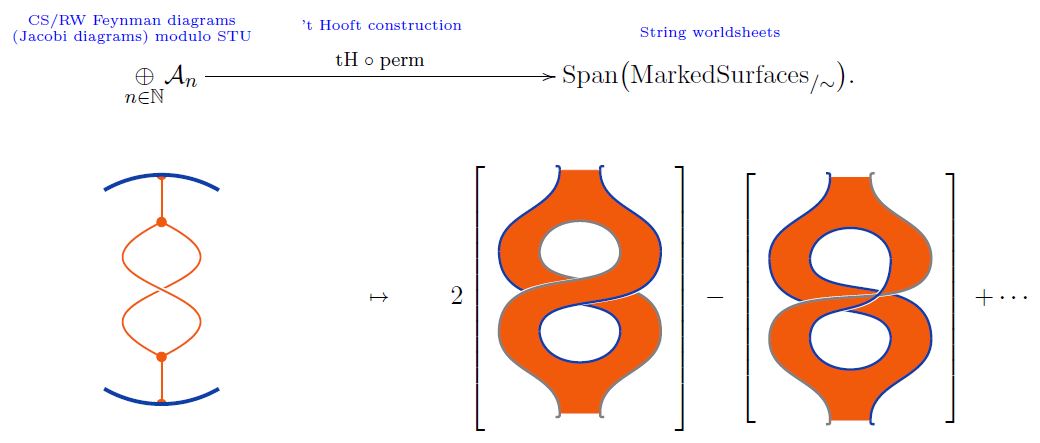
graphics from Sati-Schreiber 19c
This means that stringy weight systems pull back to ordinary weight systems along this map, corresponding to taking their point-particle limit. Under this map stringy weight systems span classical Lie algebra weight systems.
Of course, the ’t Hooft double line construction applies not just to Jacobi diagrams but also to Sullivan chord diagrams:
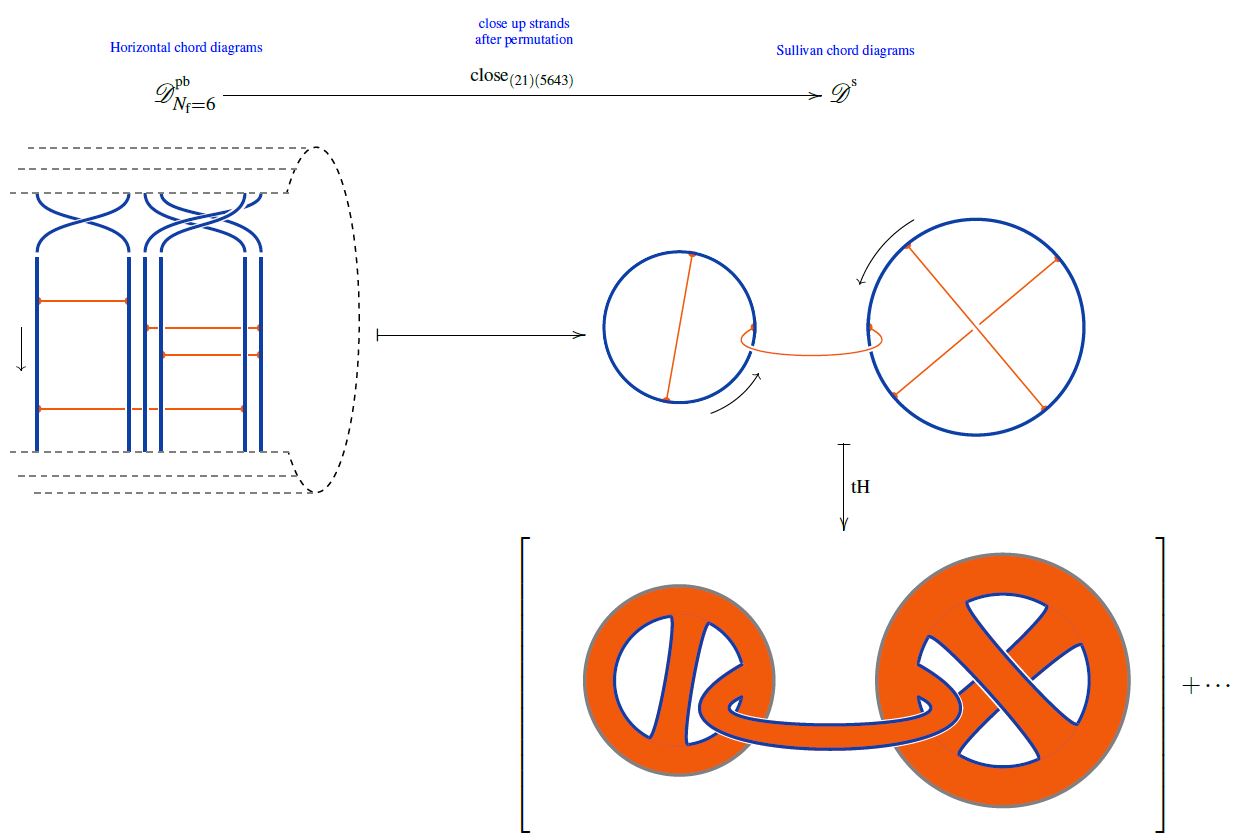
from Sati-Schreiber 19c
Applications
Large Limit and holography
One upshot of this double-line reformulation is that it makes the dependence of the Feynman amplitude on the natural number fully explicit, since a double line diagram simply contributes one factor of for each closed quark line (this being the trace over the fundamental representation).
In fact, by regarding the resulting double-line diagrams as a ribbon graph thickenings the original Feynman diagrams, and regarding these ribbon graphs in turn as surfaces, the -dependence is proportional to the genus of these surfaces.
One finds this way that in the large N limit, i.e. the limit where , precisely only the planar graphs contribute to the Yang-Mills theory Feynman amplitudes, corresponding to surfaces of genus 0 (i.e. tree level string scattering amplitudes see at planar limit for more on this), while -corrections correspond to higher worldsheet topology.
Last not least, these surfaces have the interpretation of open string worldsheets of a string theory which is “dual” to the original (super) in the sense made precise by AdS-CFT duality.
Classification of weight systems
Later the same double line technique was used (without any reference to the earlier physics articles(?)) in Bar-Natan 95, Section 6 for discussion of the classification of Lie algebra weight systems and stringy weight systems with an eye towards discussion of Vassiliev knot invariants.
Related concepts
References
General
The original article is:
- Gerard ’t Hooft, A Planar Diagram Theory for Strong Interactions, Nucl. Phys. B72 (1974) 461 (spire:80491, doi:10.1016/0550-3213(74)90154-0)
reviewed in
-
Gerard ’t Hooft, Large , workshop lecture (hep-th/0204069)
-
Markus Gross, Large , 2006 (pdf)
Generalization to arbitrary semisimple Lie algebras (semisimple Lie groups) is due to:
- Predrag Cvitanović, Group theory for Feynman diagrams in non-Abelian gauge theories, Phys. Rev. D14 (1976) 1536-1553 (doi:10.1103/PhysRevD.14.1536, spire:108133, pdf)
with a textbook account in
- Predrag Cvitanović, Group Theory: Birdtracks, Lie’s, and Exceptional Groups, Princeton University Press July 2008 (PUP, birdtracks.eu, pdf)
Discussion in the context of Vassiliev invariants and the abstract classification of Lie algebra weight systems and stringy weight systems:
-
Dror Bar-Natan, Section 6 of: On the Vassiliev knot invariants, Topology Volume 34, Issue 2, April 1995, Pages 423-472 (doi:10.1016/0040-9383(95)93237-2, pdf)
-
Dror Bar-Natan, Vassiliev and Quantum Invariants of Braids, Geom. Topol. Monogr. 4 (2002) 143-160 (arxiv:q-alg/9607001)
of which textbook accounts are in
-
Sergei Chmutov, Sergei Duzhin, Jacob Mostovoy, Introduction to Vassiliev knot invariants, Cambridge University Press, 2012 (arxiv:1103.5628, doi:10.1017/CBO9781139107846)
-
David Jackson, Iain Moffat, An Introduction to Quantum and Vassiliev Knot Invariants, Springer 2019 (doi:10.1007/978-3-030-05213-3)
Further discussion of the case of in the context of the large N limit:
-
G.M. Cicuta, Topological Expansion for and Gauge Theories, Lett. Nuovo Cim. 35 (1982) 87 (spire:177713, doi:10.1007/BF02754653)
-
Harald Ita, Harald Nieder, Yaron Oz, Perturbative Computation of Glueball Superpotentials for and , JHEP 0301:018, 2003 (arXiv:hep-th/0211261)
-
McGreevy, Swingle, Large counting, 2008 (pdf)
On the logical equivalence between the four-colour theorem and a statement about transition from the small N limit to the large N limit for Lie algebra weight systems on Jacobi diagrams via the 't Hooft double line construction:
- Dror Bar-Natan, Lie Algebras and the Four Color Theorem, Combinatorica 17-1(1997) 43–52 (arXiv:q-alg/9606016, doi:10.1007/BF01196130)
For Chern-Simons theory
Discussion of 't Hooft double line notation for Chern-Simons theory, exhibiting Chern-Simons theory as topological string theory:
-
Edward Witten, Chern-Simons Gauge Theory As A String Theory, Prog. Math. 133: 637-678, 1995 (arXiv:hep-th/9207094)
-
S. Sinha, Cumrun Vafa, and Chern-Simons at Large (arXiv:hep-th/0012136)
Open/closed string duality
On the role of open/closed string duality in interpreting the large N limit of the 't Hooft double line notation:
-
Rajesh Gopakumar, Cumrun Vafa, On the Gauge Theory/Geometry Correspondence, Adv. Theor. Math. Phys. 3 (1999) 1415-1443 (arXiv:hep-th/9811131)
-
Davide Gaiotto, Leonardo Rastelli, A paradigm of open/closed duality: Liouville D-branes and the Kontsevich model, JHEP 0507:053,2005 (hep-th/0312196)
Nowadays we interpret the 't Hooft double line notation quite literally as the perturbative expansion of an open string theory, either because the full open string theory is just equal to the gauge theory (as e.g. for Chern-Simons theory [27]), or because we take an appropriate low-energy limit (as e.g. for N = 4 SYM [31]).
The general speculation [1] is that upon summing over the number of holes, (1.1) can be recast as the genus expansion for some closed string theory of coupling . This speculation is sometimes justified by appealing to the intuition that diagrams with a larger and larger number of holes look more and more like smooth closed Riemann surfaces. This intuition is perfectly appropriate for the double-scaled matrix models, where the finite N theory is interpreted as a discretization of the closed Riemann surface; to recover the continuum limit, one must send and tune to the critical point where diagrams with a diverging number of holes dominate.
However, in AdS/CFT, or in the Gopakumar-Vafa duality [2], is a free parameter, corresponding on the closed string theory side to a geometric modulus. The intuition described above clearly goes wrong here.
A much more fitting way in which the open/closed duality may come about in these cases is for each fatgraph of genus g and with h holes to be replaced by a closed Riemann surface of the same genus g and with h punctures: each hole is filled and replaced by a single closed string insertion.
-
Rajesh Gopakumar, Free Field Theory as a String Theory?, Comptes Rendus Physique 5 (2004) 1111-1119 (hep-th/0409233)
-
Marcos Marino, Chern-Simons Theory and Topological Strings, Rev. Mod. Phys. 77:675-720, 2005 (arXiv:hep-th/0406005)
Last revised on January 24, 2020 at 14:38:49. See the history of this page for a list of all contributions to it.