nLab M2-brane
Context
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The theory of 11-dimensional supergravity contains a higher gauge field – the supergravity C-field – that naturally couples to higher electrically charged 2-branes, membranes (Bergshoeff-Sezgin-Townsend 87). By double dimensional reduction, these turn into the superstrings of type IIA string theory (Duff-Howe-Inami-Stelle 87). (See at duality between M-theory and type IIA string theory.)
When in (Witten95) it was argued that the 10-dimensional target space theories of the five types of superstring theories are all limiting cases of one single 11-dimensional target space theory that extends 11-dimensional supergravity (M-theory), it was natural to guess that this supergravity membrane accordingly yields a 3-dimensional sigma-model that reduces in limiting cases to the string sigma-models.
But there were two aspects that make this idea a little subtle, even at this vague level: first, there is no good theory of the quantization of the membrane sigma-model, as opposed to the well understood quantum string. Secondly, that hypothetical “theory extending 11-dimensional supergravity” (“M-theory”) has remained elusive enough that it is not clear in which sense the membrane would relate to it in a way analogous to how the string relates to its target space theories (which is fairly well understood).
Later, with the BFSS matrix model some people gained more confidence in the idea, by identifying the corresponding degrees of freedom in a special case (Nicolai-Helling 98, Dasgupta-Nicolai-Plefka 02). See also at membrane matrix model.
In a more modern perspective, the M2-brane worldvolume theory appears under AdS4-CFT3 duality as a holographic dual of a 4-dimensional Chern-Simons theory. Indeed, its Green-Schwarz action functional is entirely controled by the super-Lie algebra 4-cocycle of super Minkowski spacetime given by the brane scan. This exhibits the M2-brane worldvolume theory as a 3-dimensional higher dimensional WZW model.
Definition
There are two different incarnations of the M2-brane. On the one hand it is defined as a Green-Schwarz sigma model with target space a spacetime that is a solution to the equations of motion of 11-dimensional supergravity. One would call this the “fundamental” M2 in analogy with the “fundamental string”, if only there were an “M2-perturbation series” which however is essentially ruled out.
On the other hand the M2 also appears as a black brane, hence as a solution to the equations of motion of 11-dimensional supergravity with singularity that looks from outside like a charged 2 dimensional object.
As a Green-Schwarz sigma model
See at Green-Schwarz sigma model and brane scan.
As a black brane
In the absence of 4-flux
As a black brane solution to the equations of motion of 11-dimensional supergravity, with vanishing C-field flux, the M2 is the spacetime with pseudo-Riemannian metric being
where
for ;
and the field strength of the supergravity C-field is
For this is a 1/2 BPS state of 11d supergravity.
In the above coordinates the metric is ill-defined at , but in fact it may be smoothly continued through this point (Duff, Gibbons & Townsend 1994, section 3), which is an event horizon. An actual curvature singularity is at .
The near horizon geometry of this spacetime is the Freund-Rubin compactification . For more on this see at AdS-CFT.
1/2 BPS black branes in supergravity: D-branes, F1-brane, NS5-brane, M2-brane, M5-brane
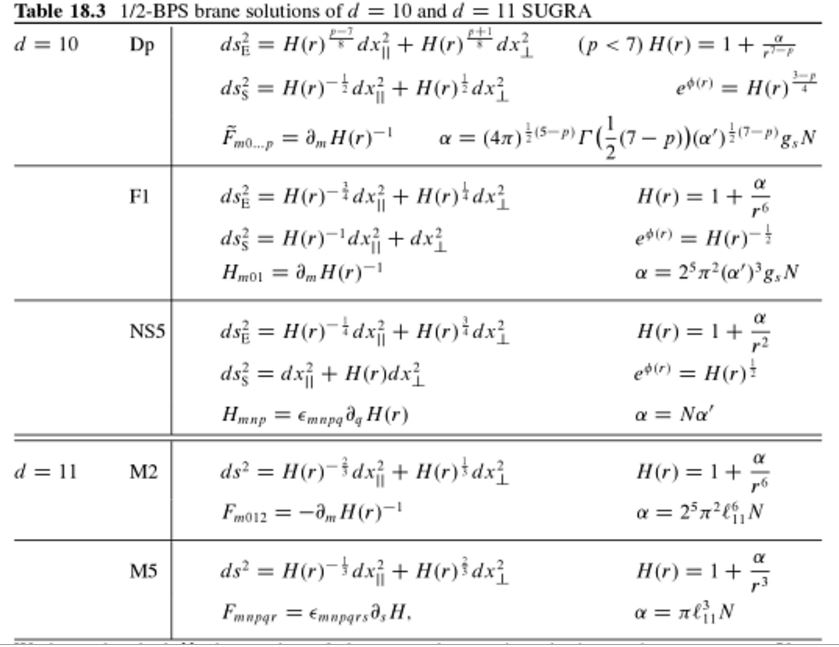
(table from Blumenhagen, Lüst & Theisen 2013, Chapter 18.5)
More generally, one may classify those solutions of 11-dimensional supergravity of the form for some closed manifold , that are at least 1/2 BPS states. One finds (Medeiros & Figueroa 2010) that all these are of the form , where is an orbifold of the 7-sphere (a spherical space form in the smooth case, see there) by a finite subgroup of SU(2) , i.e. a finite group in the ADE-classification
ADE classification and McKay correspondence
Here for -supersymmetry then the action of on is via the canonical action of as in the quaternionic Hopf fibration (Medeiros-Figueroa 10), while for then there is an extra twist to the action (MFFGME 09). See the table below.
In the presence of 4-flux
In the presence of non-vanishing C-field flux , the electric flux density of M2-branes is not alone, but receives corrections, first due to the quadratic C-field self-interaction in D=11 supergravity, but then also due to the shifted C-field flux quantization expected in M-theory:
The 11d supergravity literature states the corrected 7-flux to be the following combination, also known as the Page charge (due to Page 83 (8), Duff-Stelle 91 (43), reviewed e.g. in BLMP 13, p. 21):
where the second term subtracts the electric flux induced by the self-intersection of the field, and also ensures that the full expression is a closed differential form if the naive 11d supergravity equations of motion hold:
But in fact (1) does not quite make general sense, for two reasons:
-
In general is not an admissible condition and is not the actual vanshing of the C-field, due to the shifted C-field flux quantization.
-
Even if happens to be integrally quantizaed (if is integral) the appearance of a globally defined C-field potential in (1),means that the total flux actually does vanish after all.
Charge-quantized -flux with shifted C-field flux quantization (FSS 19b, Prop. 4.3, FSS 19c, Section 4)
Both of these issues are solved if the C-field is taken to be charge quantized in J-twisted Cohomotopy (Hypothesis H). This gives the corrected formula
where
-
the expression lives on the homotopy pullback of the Sp(2)-parametrized quaternionic Hopf fibration
to spacetime, along the twisted Cohomotopy-cocycle that represents the C-field under Hypothesis H;
-
is the integral shifted C-field pulled back to that 3-spherical fibration over spacetime;
-
trivializes not the C-field itself, but its pullback, and not absolutely but relative to the background charge implied by shifted C-field flux quantization.
With the corrected 7-flux in twisted Cohomotopy it becomes true that
-
the integral of around the 7-sphere linking a black M2-brane is always integer (FSS 19c, Theorem 4.6);
-
this integer satisfies the C-field tadpole cancellation condition (FSS 19b, Section 4.6).
Properties
Quantization via BFSS matrix model
A regularized quantization of the Green-Schwarz sigma-model for the M2-brane yields the BFSS matrix model (Nicolai-Helling 98, Dasgupta-Nicolai-Plefka 02).
In this correspondence, matrix blocks around the diagonal correspond to blobs of membrane, while off-diagonal matrix elements correspond to thin tubes of membrane connecting these blobs.
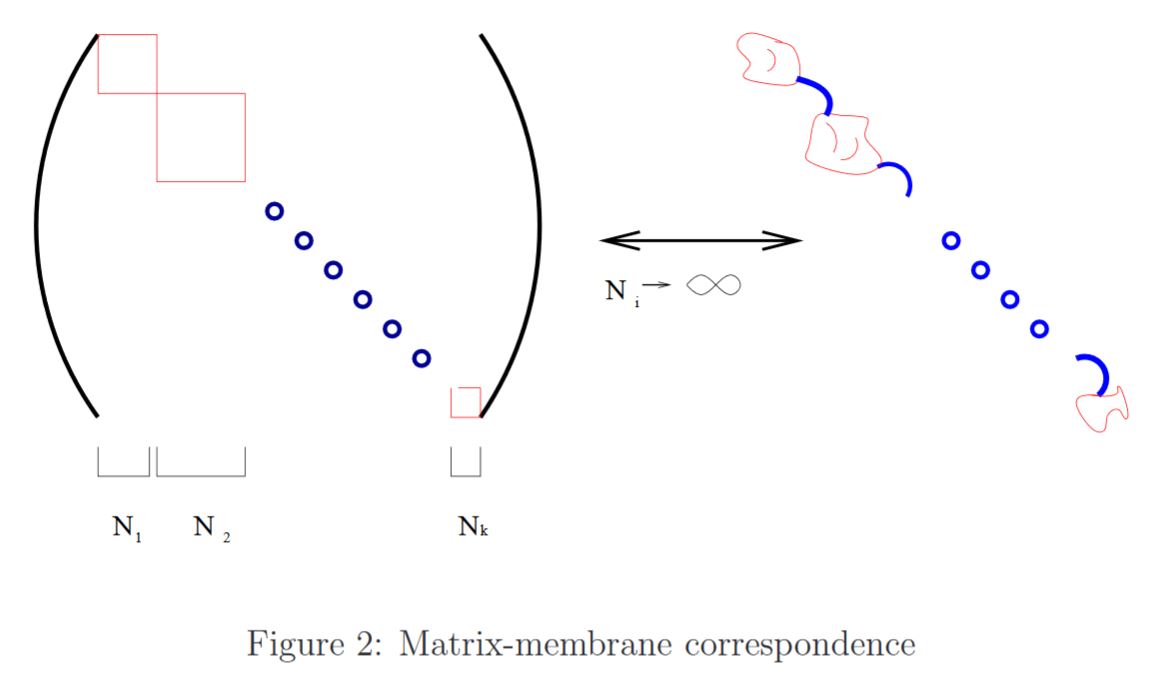
graphics grabbed from Dasgupta-Nicolai-Plefka 02
Worldvolume theory – BLG and ABJM
The worldvolume QFT of black M2-branes is a 3d superconformal gauge field theory:
(Shnider 88, also Nahm 78, see Minwalla 98, section 4.2)
Specifically, worldvolume quantum field theory of M2-branes sitting at ADE singularities (as above) is supposed to be described by ABJM theory and, for the special case of gauge group, by the BLG model. See also at gauge enhancement.
- José Figueroa-O'Farrill et al. 2009 (arXiv:0909.0163, pdf slides)
AdS4-CFT3 duality
Under AdS-CFT duality the M2-brane is given by AdS4-CFT3 duality. (Maldacena 97, section 3.2, Klebanov-Torri 10).
M2/M5 bound states
For M2-M5 brane bound states, i.e. bound states of M2-branes with M5-branes (dyonic M2-branes and giant gravitons), see the references below.
For the type II string theory-version see at NS5-brane the sectoin NS5/D4/D2 bound states.
M2-M5 brane bound states in the BMN matrix model
There is the suggestion (MSJVR 02, checked in AIST 17a, AIST 17b) that, in the BMN matrix model, supersymmetric M2-M5-brane bound states are identified with isomorphism classes of certain “limit sequences” of longitudinal-light cone-constant -matrix-fields constituting finite-dimensional complex Lie algebra representations of su(2).
Traditional discussion
Concretely, if
denotes the representation containing
of the
(for some finitely indexed set of pairs of natural numbers)
with total dimension
then:
-
a configuration of a finite number of stacks of coincident M5-branes corresponds to a sequence of such representations for which
-
(this being the relevant large N limit)
-
for fixed (being the number of M5-branes in the th stack)
-
and fixed ratios (being the charge/light-cone momentum carried by the th stack);
-
-
an M2-brane configuration corresponds to a sequence of such representations for which
-
(this being the relevant large N limit)
-
for fixed (being the number of M2-brane in the th stack)
-
and fixed ratios (being the charge/light-cone momentum carried by the th stack)
-
for all .
Hence, by extension, any other sequence of finite-dimensional -representations is a kind of mixture of these two cases, interpreted as an M2-M5 brane bound state of sorts.
Formalization via weight systems on chord diagrams
To make this precise, let
be the set of isomorphism classes of complex metric Lie representations (hence finite-dimensional representations) of su(2) (hence of the special linear Lie algebra ) and write
for its linear span (the complex vector space of formal linear combinations of isomorphism classes of metric Lie representations).
Finally, write
for the linear map which sends a formal linear combination of representations to the weight system on Sullivan chord diagrams with chords which is given by tracing in the given representation.
Then a M2-M5-brane bound state as in the traditional discussion above, but now formalized as an su(2)-weight system
hence a weight system horizontal chord diagrams closed to Sullivan chord diagrams, these now being the multi-trace observables on these) is

(from Sati-Schreiber 19c)
Normalization and large limit. The first power of the square root in (3) reflects the volume measure on the fuzzy 2-sphere (by the formula here), while the power of (which is the number of operators in the multi-trace observable evaluating the weight system) gives the normalization (here) of the functions on the fuzzy 2-sphere.
Hence this normalization is such that the single-trace observables among the multi-trace observables, hence those which come from round chord diagrams, coincide on those M2-M5 brane bound states for which , hence those which have a single constitutent fuzzy 2-sphere, with the shape observables on single fuzzy 2-spheres discussed here:

(from Sati-Schreiber 19c)
Therefore, with this normalization, the limits and of (3) should exist in weight systems. The former trivially so, the latter by the usual convergence of the fuzzy 2-sphere to the round 2-sphere in the large N limit.
Notice that the multi trace observables on these states only see the relative radii of the constitutent fuzzy 2-spheres: If then the -dependence of (3) cancels out, reflecting the fact that then there is only a single constituent 2-sphere of which the observable sees only the radius fluctuations, not the absolute radius (proportional to ).
Related concepts
Table of branes appearing in supergravity/string theory (for classification see at brane scan).
References
- Mike Duff, chapter 2 of: The World in Eleven Dimensions: Supergravity, Supermembranes and M-theory, IoP (1999) [ISBN:9780750306720]
Super-membrane/M2-brane as a sigma model
The Green-Schwarz sigma-model-type formulation of the super-membrane in 11d (as in the brane scan and in contrast to the black brane-solutions of 11d supergravity) first appears in:
- Eric Bergshoeff, Ergin Sezgin, Paul Townsend: Supermembranes and eleven-dimensional supergravity, Phys. Lett. B 189 (1987) 75-78 [doi:10.1016/0370-2693(87)91272-X, spire:248230]
Via the superembedding approach the equations of motion were obtained in
- Igor Bandos, Paolo Pasti, Dmitri Sorokin, Mario Tonin, Dmitry Volkov, Chapter 3 of Superstrings and supermembranes in the doubly supersymmetric geometrical approach, Nucl. Phys. B446:79-118, 1995 (arXiv:hep-th/9501113)
and the Lagrangian density in:
- Paul Howe, Ergin Sezgin, The supermembrane revisited, Class. Quant. Grav. 22 (2005) 2167-2200 [arXiv:hep-th/0412245, doi:10.1088/0264-9381/22/11/017]
The double dimensional reduction of the M2-brane to the Green-Schwarz superstring was observed in
-
Michael Duff, Paul Howe, T. Inami, Kellogg Stelle, Superstrings in from Supermembranes in , Phys. Lett. B 191 (1987) 70 [doi:10.1016/0370-2693(87)91323-2]
also in: Michael Duff (ed.): The World in Eleven Dimensions 205-206 (1987) [spire:245249]
-
Paul Townsend, The eleven-dimensional supermembrane revisited, Phys. Lett. B 350 (1995) 184-187 [arXiv:hep-th/9501068, doi:10.1016/0370-2693(95)00397-4]
around the time when M-theory became accepted due to
On the early history of these developments:
- Eric A. Bergshoeff, Ergin Sezgin, Paul K. Townsend: A brief history of supermembranes [arXiv:2503.06234]
See also:
-
Igor Bandos, Paul Townsend, SDiff Gauge Theory and the M2 Condensate (arXiv:0808.1583)
-
Maria P. Garcia del Moral, C. Las Heras, P. Leon, J. M. Pena, Alvaro Restuccia, Fluxes, Twisted tori, Monodromy and Supermembranes, J. High Energ. Phys. 2020 97 (2020) [arXiv:2005.06397, doi:10.1007/JHEP09(2020)097]
Discussion from the point of view of Green-Schwarz action functional-∞-Wess-Zumino-Witten theory:
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields (2013)
On possible structures in M2-brane dynamics and M2-M5-brane bound states which could be M-theory-lifts of the familiar integrability of the Green-Schwarz superstring on :
- Kirill Gubarev, Edvard Musaev, Integrability structures in string theory [arXiv:2301.06486]
Quantization of the M2-brane sigma-model to a matrix model
The Poisson bracket-formulation of the classical light-cone gauge Hamiltonian for the bosonic relativistic membrane and the corresponding matrix commutator regularization is due to:
- Jens Hoppe, Quantum theory of a massless relativistic surface and a two-dimensional bound state problem, MIT 1982 (dspace:1721.1/15717, pdf)
Some exact solutions:
-
Jens Hoppe, Exact algebraic M(em)brane solutions arXiv:2107.00569
-
Jens Hoppe, The fast non-commutative sharp drop arXiv:2302.13146
On the regularized light-cone gauge quantization of the Green-Schwarz sigma model for the M2-brane on (super) Minkowski spacetime, yielding the BFSS matrix model:
Original articles:
- Bernard de Wit, Jens Hoppe, Hermann Nicolai, On the Quantum Mechanics of Supermembranes, Nucl. Phys. B 305 (1988) 545-581 [doi:10.1016/0550-3213(88)90116-2, spire:261702, pdf, pdf]
Observation that the spectrum is continuous:
- Bernard de Wit, W. Lüscher, Hermann Nicolai, The supermembrane is unstable, Nucl. Phys. B 320 (1989) 135 [doi:10.1016/0550-3213(89)90214-9, spire:266584]
Review:
-
Hermann Nicolai, Robert C. Helling, Supermembranes and M(atrix) Theory, In: Trieste 1998, Nonperturbative aspects of strings, branes and supersymmetry (1998) 29-74 (arXiv:hep-th/9809103, spire:476366)
-
Jens Hoppe, Membranes and Matrix Models [arXiv:hep-th/0206192]
-
Arundhati Dasgupta, Hermann Nicolai, Jan Plefka, An Introduction to the Quantum Supermembrane, Grav. Cosmol. 8 1 (2002) and Rev. Mex. Fis. 49S1 (2003) 1-10 [arXiv:hep-th/0201182, spire:582067]
-
Gijs van den Oord, On Matrix Regularisation of Supermembranes MSc thesis (2006) (pdf)
-
Meer Ashwinkumar, Lennart Schmidt, Meng-Chwan Tan, Section 2 of: Matrix Regularization of Classical Nambu Brackets and Super -Branes (arXiv:2103.06666)
The generalization to pp-wave spacetimes (leading to the BMN matrix model):
-
Keshav Dasgupta, Mohammad Sheikh-Jabbari, Mark Van Raamsdonk, Section 2 of: Matrix Perturbation Theory For M-theory On a PP-Wave, JHEP 0205:056, 2002 (arXiv:hep-th/0205185)
-
Keshav Dasgupta, Mohammad Sheikh-Jabbari, Mark Van Raamsdonk, Section 2 of: Matrix Perturbation Theory For M-theory On a PP-Wave, JHEP 0205:056, 2002 (arXiv:hep-th/0205185)
See also
-
Mike Duff, T. Inami, Christopher Pope, Ergin Sezgin, Kellogg Stelle, Semiclassical Quantization of the Supermembrane, Nucl.Phys. B297 (1988) 515-538 (spire:247064)
-
Daniel Kabat, Washington Taylor, section 2 of: Spherical membranes in Matrix theory, Adv. Theor. Math. Phys. 2: 181-206, 1998 (arXiv:hep-th/9711078)
-
Nathan Berkovits, Towards Covariant Quantization of the Supermembrane (arXiv:hep-th/0201151)
-
Qiang Jia, On matrix description of D-branes (arXiv:1907.00142)
A new kind of perturbation series for the quantized super-membrane:
- Olaf Lechtenfeld, Hermann Nicolai, A perturbative expansion scheme for supermembrane and matrix theory (arXiv:2109.00346)
Relation to the string dilaton under double dimensional reduction:
- Krzysztof A. Meissner, Hermann Nicolai, Fundamental Membranes and the String Dilaton, J. High Energ. Phys. 2022 219 (2022) arXiv:2208.05822, doi:10.1007/JHEP09(2022)219
As a black brane
The black membrane solution of 11-dimensional supergravity was found in
- Mike Duff, Kellogg Stelle, Multi-membrane solutions of supergravity, Phys. Lett. B 253 1-2 (1991) 113-118 [spire:299386, doi:10.1016/0370-2693(91)91371-2]
Its regularity across the event horizon is due to
- Mike Duff, Gary Gibbons, Paul Townsend: Macroscopic superstrings as interpolating solitons, Phys. Lett. B 332 (1994) 321-328 [arXiv:hep-th/9405124]
Further discussion of such Freund-Rubin compactifications:
- Don Page, Classical stability of round and squashed seven-spheres in eleven-dimensional supergravity, Phys. Rev. D 28 12 (1983) 2976-2982 [spire:14480, doi:10.1103/PhysRevD.28.2976]
The Horava-Witten-orientifold of the black M2, supposedly yielding the black heterotic string is discussed in
-
Zygmunt Lalak, André Lukas, Burt Ovrut, Soliton Solutions of M-theory on an Orbifold, Phys. Lett. B425 (1998) 59-70 (arXiv:hep-th/9709214)
-
Ken Kashima, The M2-brane Solution of Heterotic M-theory with the Gauss-Bonnet terms, Prog.Theor.Phys. 105 (2001) 301-321 (arXiv:hep-th/0010286)
Meanwhile AdS-CFT duality was recognized in
- Juan Maldacena, The Large N limit of superconformal field theories and supergravity, Adv. Theor. Math. Phys. 2:231, 1998, hep-th/9711200;
where a dual description of the worldvolume theory of M2-brane appears in section 3.2. More on this is in
- Igor Klebanov, Giuseppe Torri, M2-branes and AdS/CFT, Int.J.Mod.Phys.A25:332-350,2010 (arXiv:0909.1580)
An account of the history as of 1999 is in
- Mike Duff, chapter II of The World in Eleven Dimensions: Supergravity, Supermembranes and M-theory, IoP 1999 (publisher)
More recent review is in
- Georgios Linardopoulos, chapter 13 of Classical Strings and Membranes in the AdS/CFT Correspondence (pdf, spire)
A detailed discussion of this black brane-realization of the M2-brane and its relation to AdS-CFT is in
- Gianguido Dall'Agata, Davide FabbKri, Christophe Fraser, Pietro Fré, Piet Termonia, Mario Trigiante, The singleton action from the supermembrane, Nucl.Phys.B542:157-194, 1999 (arXiv:hep-th/9807115)
The generalization of this to BPS sugra solutions of the form is due to
-
Paul de Medeiros, José Figueroa-O'Farrill, Sunil Gadhia, Elena Méndez-Escobar: Half-BPS quotients in M-theory: ADE with a twist, JHEP 0910 038 (2009) [arXiv:0909.0163, pdf slides]
-
Paul de Medeiros, José Figueroa-O'Farrill: Half-BPS M2-brane orbifolds, Adv. Theor. Math. Phys. 16 5 (2012) 1349-1408 [arXiv:1007.4761, euclid:atmp/1408561553]
Further solutions:
- A. M. Ghezelbash, M-Branes on Minimal Surfaces [arXiv:2407.07855]
See also:
- Fridrik Freyr Gautason, Jesse van Muiden: Localisation of the M2-brane [arXiv:2503.16597]
In
Review:
- Kazuo Hosomichi, M2-branes and AdS/CFT: A Review [arXiv:2003.13914]
History
- Mike Duff:
M-history without the M [arXiv:1501.04098]
Decoupled worldvolume theory
On the BLG model/ABJM model for the worldvolume-theory of coincident M2-branes see there.
Review:
- Jonathan Bagger, Neil Lambert, Sunil Mukhi, Constantinos Papageorgakis, Multiple Membranes in M-theory, Physics Reports, Volume 527, Issue 1, 1 June 2013, Pages 1-100 (arXiv:1203.3546, doi:10.1016/j.physrep.2013.01.006)
Dualities
The role of and the relation to duality in string theory of the membrane is discussed in the following articles.
Relation to T-duality is discussed in:
-
J.G. Russo, T-duality in M-theory and supermembranes (arXiv:hep-th/9701188)
-
M.P. Garcia del Moral, J.M. Pena, A. Restuccia, T-duality Invariance of the Supermembrane (arXiv:1211.2434)
Relation to U-duality is discussed in:
-
Martin Cederwall, M-branes on U-folds (arXiv:0712.4287)
-
M.P. Garcia del Moral, Dualities as symmetries of the Supermembrane Theory (arXiv)
Discussion from the point of view of E11-U-duality and current algebra is in
-
Hirotaka Sugawara, Current Algebra Formulation of M-theory based on E11 Kac-Moody Algebra, International Journal of Modern Physics A, Volume 32, Issue 05, 20 February 2017 (arXiv:1701.06894)
-
Shotaro Shiba, Hirotaka Sugawara, M2- and M5-branes in Current Algebra Formulation of M-theory (arXiv:1709.07169)
M2-M5 bound states
Discussion of M2-M5 brane bound states, i.e. dyonicblack M2-branes (M5-branes wrapped on a 3-manifold, see also at NS5-branes – D2/D4/NS5-bound states):
-
J.M. Izquierdo, Neil Lambert, George Papadopoulos, Paul Townsend, Dyonic Membranes, Nucl. Phys. B460:560-578, 1996 (arXiv:hep-th/9508177)
-
Michael Green, Neil Lambert, George Papadopoulos, Paul Townsend, Dyonic -branes from self-dual -branes, Phys. Lett. B384:86-92, 1996 (arXiv:hep-th/9605146)
-
Troels Harmark, Section 3.1 of Open Branes in Space-Time Non-Commutative Little String Theory, Nucl.Phys. B593 (2001) 76-98 (arXiv:hep-th/0007147)
-
Troels Harmark, N.A. Obers, Section 5.1 of Phase Structure of Non-Commutative Field Theories and Spinning Brane Bound States, JHEP 0003 (2000) 024 (arXiv:hep-th/9911169)
-
George Papadopoulos, Dimitrios Tsimpis, The holonomy of the supercovariant connection and Killing spinors, JHEP 0307:018, 2003 (arXiv:hep-th/0306117)
-
Nicolò Petri, slide 14 of Surface defects in massive IIA, talk at Recent Trends in String Theory and Related Topics 2018 (pdf)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Section 4 of Twisted Cohomotopy implies M-theory anomaly cancellation (arXiv:1904.10207)
-
Jay Armas, Vasilis Niarchos, Niels A. Obers, Thermal transitions of metastable M-branes (arXiv:1904.13283)
Further M2/M5-brane bound states to giant gravitons:
- J. M. Camino, A. V. Ramallo, M-Theory Giant Gravitons with C field, Phys. Lett. B525:337-346, 2002 (arXiv:hep-th/0110096)
Last revised on March 24, 2025 at 05:30:44. See the history of this page for a list of all contributions to it.