nLab braid group statistics
Context
Topological physics
Topological Physics – Phenomena in physics controlled by the topology (often: the homotopy theory) of the physical system.
General theory:
In metamaterials:
For quantum computation:
Quantum systems
-
quantum algorithms:
Contents
- Anyon braiding
- As generalized boson/fermion statistics?
- Braiding of anyonic quanta – via “fictitious” AB-phases
- Braiding of anyonic defects – via adiabatic Berry phases
- Related concepts
- References
- General
- Anyonic topological order in terms of braided fusion categories
- Anyons in fractional quantum Hall systems
- Observation of anyons in fractional quantum Hall systems
- Superconducting defect anyons in FQH systems
- Anyons in topological superconductors
- Defect anyons
- Anyons in momentum-space
- Topological quantum computation with anyons
- Braid group representations (as topological quantum gates)
- Compilation to braid gate circuits
Anyon braiding
In quantum physics, braid group statistics or anyon statistics (sometimes: plektons) refers to an exotic kind of particle statistics where the braiding of the worldlines of certain effective particles (“anyons”) in an effectively 1+2-dimensional spacetime has the effect of transforming the quantum state of the total quantum system by unitary operators which constitute a linear representation of the braid group – a braid representation.
Often this is motivated as a generalization of the boson- or fermion-“statistics” which enters the spin-statistics theorem, see below.
But the actual mathematical nature of anyons must be different from that of elements of boson/fermion-Fock spaces and often remains somewhat vague in existing discussions. One may recognize two different more concrete conceptualizations of anyons in the literature:
-
anyonic quanta much like boson/fermion quanta but subject to an additional global interaction by Aharonov-Bohm phases due to a flat fictitious gauge field which is sourced by and coupled to each of the quanta;
(this goes back to Arovas, Schrieffer, Wilczek & Zee 1985, further developed in Chen, Wilczek, Witten & Halperin 1989, see below)
-
anyonic defects like vortices or other solitons, whose position is a classical parameter to the quantum system, the adiabatic movement of which acts by Berry phases on the quantum ground state.
(e.g. Arovas, Schrieffer & Wilczek 1984, see further below)
The concept of anyons is particularly well motivated in solid state physics, where effectively 2-dimensional quantum materials are common place (eg. graphene) or where particles may otherwise be constrained to move in a plane, such as in the quantum Hall effect. There is a multitude of models in condensed matter theory (mostly lattice models, such as string-net models) which theoretically realize anyon braid group statistics, and there are some first experimental indications of anyonic phenomena in actual materials (see the references under Experimental Realization) below.
Specifically, in the context of topological phases of matter, the (potential) presence of anyons has come to be known as the case of topological order, see there for more.
Besides general curiosity, much of the interest in anyonic braid group statistics lies in the fact that these braid representations are imagined to potentially serve as quantum gates in topological quantum computers. See there for more.
As generalized boson/fermion statistics?
In quantum field theory, one speaks of the “statistics” of a particle species when referring to the linear representation that -particle wavefunctions form under the the symmetric group which permutes the particles.
While there is a rich representation theory of the symmetric group, the spin-statistics theorem says, when it applies, that for field quanta only the simplest two possibilities may occur:
-
bosons (such as photons) transform under the trivial representation of ,
-
fermions (such as electrons) transform under the sign representation of .
(see also at Slater determinant)
Now, the braid group on strands covers the symmetric group
which allows one to regard any linear representation of the symmetric group also as a particular braid group representation. But by its definition, the braid group may be understood as the group of isotopy-classes of disjoint timelike worldlines in an effectively 2+1 dimensional spacetime, with the group operation being concatenation of worldlines.
In this sense, one may imagine that any braid group representations may generalize the boson/fermion statistics in 2+1 dimensions. Texts typically suggest that this applies to quasiparticles.
The term anyon (due to Wilczek 1982b) is a pun on this state of affairs that any statistics “in between” boson- and fermion-statistics may be allowed.
On the other hand, anyonic braiding is conceptually different from boson/fermion statistics – if it were on the same footing then the spin-statistics theorem would rule out anyonic braiding. This is acknowledged by Chen, Wilczek, Witten & Halperin 1989, p. 352 (cf. also Wilczek 1990, §I.2, pp. 11):
Once the permutation group is replaced by the braid group, the simple construction of passing from the solution to the one-particle problems to the solution of many-particle problems, familiar from the free bosons and free fermions, does not work anymore.
Braiding of anyonic quanta – via “fictitious” AB-phases
A concrete model for anyonic quanta via otherwise free fermions in 2d interacting through a flat “fictitious gauge field” was proposed in Arovas, Schrieffer, Wilczek & Zee 1985 and developed in Chen, Wilczek, Witten & Halperin 1989 and Iengo & Lechner 1992 (the model has been advertized in early reviews, e.g. Wilczek 1990, §I.3 and Wilczek 1991, but seems not to have been developed much since):
This model regards anyons as a priori free fermions, but equipped now with a non-local mutual interaction via a “fictitious gauge field” (CWWH89, §2), in that each of the particles is modeled as the singular source of a flat circle connection (a vector potential with vanishing field strength), which hence exerts no Lorentz force but has the effect that globally each other particle is subject to the same Aharonov-Bohm effect as would be caused by a tuple of infinite solenoids piercing through each of the other particle’s positions.
For emphasis, from CWWH89, p. 359:
Here the particles are to be regarded (in the absence of interactions) as fermions; the interaction then makes them anyons with statistical parameter .
It follows (Wu 1984, Imbo, Imbo & Sudarshan 1990) that (quoting from Fröhlich, Gabbiani & Marchetti 1990, p. 20):
If the Hilbert space of anyon wave functions must be chosen to be a space of multi-valued functions with half-monodromies given by the phase factors . Such wave functions can be viewed as single-valued functions on the universal cover of [the configuration space of points&rbrack.
Further discussion of anyon-wavefunctions as multi-valued functions on a configuration space of points, hence equivariant functions on its universal cover: BCMS93, §1, Mund & Schrader 1995, DFT97, §1 Myrheim 1999, DMV03, Murthy & Shankar 2009
Incidentally, the quasi-particle-excitations of (or in) a gas of such Aharonov-Bohm phased anyons are argued to be vortices (CWWH89, p. 457):
we are led to conclude that in anyon superconductivity, charged quasi-particles and vortices do not constitute two separate sorts of elementary excitations - they are one and the same.
This seamlessly leads over to:
Braiding of anyonic defects – via adiabatic Berry phases
In practice, many (most?) incarnations of the concept of anyons are anyonic defects – non-perturbative solitonic defects (of codimension=2), akin to vortices in fluids:
Anyonic particles are best viewed as a kind of topological defects that reveal non-trivial properties of the ground state. [Kitaev 2006, p. 4]
Anyons can arise in two ways: as localised excitations of an interacting quantum Hamiltonian or as defects in an ordered system. [Das Sarma, Freedman & Nayak 2015, p. 1]
(Compare also the original discussions in Goldin, Menikoff & Sharp 1981, §III, Wilczek 1982a & Wilczek 1990, p. 5, which offer a quantum particle “bound” to a classical & infinite solenoid – hence a 2d magnetic monopole defect – as a decent model for an anyon.)
But defects are a kind of boundary conditions, hence external parameters or background fields for the actual quantum field.
Concretely, a widely appreciated proposal (Moore & Read 1991, Read & Rezayi 1999) identifies anyonic ground state wavefunctions with conformal blocks of a 2d CFT – hence with Chern-Simons theory states – with prescribed poles at the location of the anyons.
Now the quantum adiabatic theorem says that the sufficiently slow motion of such external parameters transforms the quantum ground state by unitary operators (“Berry phases”, see also at adiabatic quantum computation). This suggests (Arovas, Schrieffer & Wilczek 1984, p. 1, Freedman, Kitaev, Larsen & Wang 2003, pp. 6, Nayak, Simon, Stern & Freedman 2008, §II.A.2 (p. 6), Cheng, Galitski & Das Sarma 2011, p. 1) that:
Definition
(adiabatic defect braiding)
Anyon braiding statistics is the braid group representation on a quantum ground state induced by adiabatic braiding of topological codimension=2 defects in their configuration space.
Here
-
for point-defects the “configuration space” is the configuration space of points in a surface (as briefly touched upon already in Leinaas & Myrheim 1977, pp. 22, Wilczek 1982b, p. 959), such as in the plane, in which case its fundamental group is the braid group;
-
“topological” is meant as in topological quantum field theory: The induced adiabatic unitary transformation is demanded/assumed to depend only on the isotopy-class of the defect-worldlines, hence only on the underlying braid-pattern.
This notion of anyon “statistics” is at least tacitly implicit in much of the literature on anyons in topological quantum computation, such as in the popular graphics depicting anyon worldlines as the Wilson lines in Chern-Simons theory. (see the graphics below).
Indeed, the effects of adiabatic braiding of defects in quantum materials has been understood and discussed before and in parallel to the term “anyon” becoming established: Mermin 1979, Lo & Preskill 1993.
A concrete realistic example of defect anyons are vortex anyons see below. But the notion of codimension=2 defects subsumes situations that are quite different from the quasiparticle-excitations imagined in traditional texts on anyons, such as:
Vortex anyons
Specifically, vortex anyons are realized in Bose-Einstein condensates (MPSS19, following PFCZ01) and in (other) superfluids (MMN21).
In fact, defect-type vortex anyons generically appear in condensates of non-defect anyons (CDLR19):
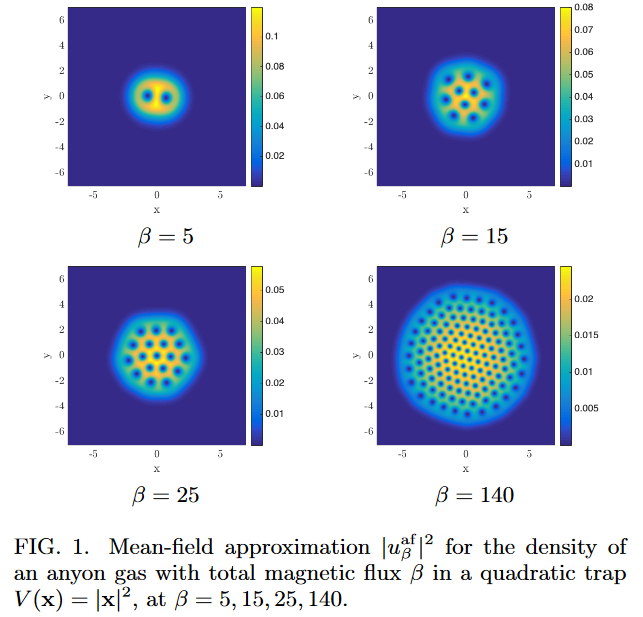
A theoretical model of vortex anyons in a Higgs field coupled to Chern-Simons theory is discussed in Fröhlich & Marchetti 1988. An instructive lattice model of vortex anyons is analyzed in detail in Kitaev 2006.
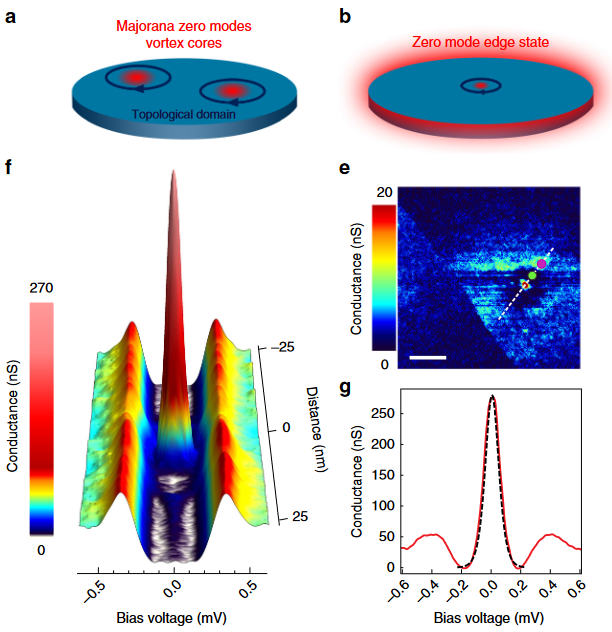
Much attention in current efforts towards realizing topological quantum computation is being paid to anyons realized as Majorana zero modes bound to vortices (Das Sarma, Freedman & Nayak 2015, cf. MMBDRSC19).
This situation may generalize to parafermion-su(2)-anyons, where
each (anti)soliton carries parafermion zero mode which supplies it with the non-Abelian statistics [Tsvelik 2014a, p. 2, cf. Borcherding 2018, pp. 3].
Braiding of nodal points in momentum space (graphics from MMBDRSC19, Fig. 1):
Anyonic band nodes?
Around 2020 the view has been emerging that also defects “in momentum/reciprocal space” may behave as anyonic defects under braiding in momentum space. This applies concretely to nodal points (where electron bands touch or cross) in the momentum space Brillouin torus of topological semi-metals:
here are band crossing points, henceforth called vortices [Ahnm Park & Yang 2019]
a new type non-Abelian “braiding” of nodal-line rings inside the momentum space [Tiwari & Bzdušek 2020]
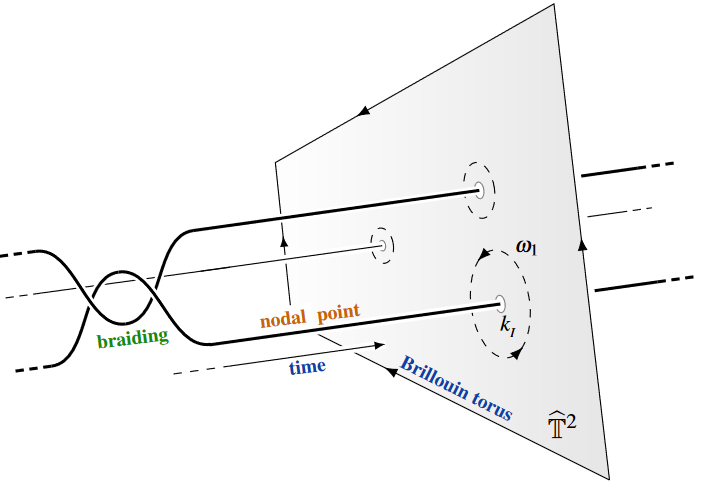
(graphics from SS22)
Curiously, these reciprocal/momemtum space anyons lend themselves to tractable laboratory manipulation in a way that has remained notoriously elusive for “position space” anyons:
Our work opens up routes to readily manipulate Weyl nodes using only slight external parameter changes, paving the way for the practical realization of reciprocal space braiding [CBSM22],
specifically
it is possible to controllably braid Kagome band nodes in monolayer using strain and/or an external electric field [PBMS22],
leading to:
new opportunities for exploring non-Abelian braiding of band crossing points (nodes) in reciprocal space, providing an alternative to the real space braiding exploited by other strategies.
Real space braiding is practically constrained to boundary states, which has made experimental observation and manipulation difficult; instead, reciprocal space braiding occurs in the bulk states of the band structures and we demonstrate in this work that this provides a straightforward platform for non-Abelian braiding. [PBSM22].
Defect branes
In string theory, defect branes are D-branes or M-branes of codimension=2, such as D7-branes in type IIB string theory or M5-brane-intersections on “M3-branes” in M-theory.
It has been suggest in deBoer & Shigemori 2012, p. 65 that these could behave like anyons. This is further substantiated in SS22. See there for more.
Related concepts
References
General
The concept of anyons satisfying braid group statistics originated independently in:
-
Jon Magne Leinaas, Jan Myrheim, On the theory of identical particles, К теории тождествениых частиц, Nuovo Cim B 37, 1–23 (1977) (doi:10.1007/BF02727953)
-
G. A. Goldin, R. Menikoff, D. H. Sharp, Representations of a local current algebra in nonsimply connected space and the Aharonov–Bohm effect, J. Math. Phys. 22 1664 (1981) [doi:10.1063/1.525110]
-
Frank Wilczek, Magnetic Flux, Angular Momentum, and Statistics, Phys. Rev. Lett. 48 (1982) 1144 (reprinted in Wilczek 1990, p. 163-165) [doi:10.1103/PhysRevLett.48.1144]
The term anyon was introduced in:
- Frank Wilczek, Quantum Mechanics of Fractional-Spin Particles, Phys. Rev. Lett. 49 (1982) 957 (reprinted in Wilczek 1990, p. 166-168) [doi:10.1103/PhysRevLett.49.957]
Identification of anyon phases (specifically in the quantum Hall effect) as Berry phases of an adiabatic transport of anyon positions:
- Daniel P. Arovas, John Robert Schrieffer, Frank Wilczek, Fractional Statistics and the Quantum Hall Effect, Phys. Rev. Lett. 53 7 (1984) 722-723 [doi:10.1103/PhysRevLett.53.722]
The “fictitious gauge field”-method for modelling anyons:
-
Daniel P. Arovas, Robert Schrieffer, Frank Wilczek, Anthony Zee, Statistical mechanics of anyons, Nuclear Physics B 251 (1985) 117-126 (reprinted in Wilczek 1990, p. 173-182) [doi:10.1016/0550-3213(85)90252-4]
-
Yi-Hong Chen, Frank Wilczek, Edward Witten, Bertrand Halperin, On Anyon Superconductivity, International Journal of Modern Physics B 03 07 (1989) 1001-1067 (reprinted in Wilczek 1990, p. 342-408) [doi:10.1142/S0217979289000725, pdf]
-
Frank Wilczek, States of Anyon Matter, International Journal of Modern Physics B 05 09 (1991) 1273-1312 [doi:10.1142/S0217979291000626]
and with specific emphasis on the resulting (abelian!) Chern-Simons theory:
- Roberto Iengo, Kurt Lechner: Anyon quantum mechanics and Chern-Simons theory, Physics Reports 213 4 (1992) 179-269 [doi:10.1016/0370-1573(92)90039-3]
The suggestion that the anyonic ground state-wavefunctions are essentially conformal blocks of 2d CFT (notably for su(2)-anyons):
-
Gregory Moore, Nicholas Read, Nonabelions in the fractional quantum hall effect, Nuclear Physics B 360 2–3 (1991) 362-396 [doi:10.1016/0550-3213(91)90407-O, pdf]
-
Nicholas Read, Edward Rezayi, Beyond paired quantum Hall states: Parafermions and incompressible states in the first excited Landau level, Phys. Rev. B 59 (1999) 8084 [doi:10.1103/PhysRevB.59.8084]
More comprehensive accounts of anyons:
-
Frank Wilczek, Fractional Statistics and Anyon Superconductivity, World Scientific (1990) [doi:10.1142/0961]
-
Alexei Kitaev, Anyons in an exactly solved model and beyond, Annals of Physics 321 1 (2006) 2-111 [doi:10.1016/j.aop.2005.10.005, arXiv:cond-mat/0506438]
-
Eduardo Fradkin, Anyon superconductivity, Chapter 11 in: Field Theories of Condensed Matter Physics, Cambridge University Press (2013) 414-431 [ISBN: 9781139015509, doi:10.1017/CBO9781139015509.013]
-
Eduardo C. Marino: Non-Abelian Statistics and Quantum Computation, chapter 30 in: Quantum Field Theory Approach to Condensed Matter Physics, Cambridge University Press (2017) [doi:10.1017/9781139696548]
See also:
-
Martin Greiter, Frank Wilczek: Fractional Statistics, Annual Review of Condensed Matter Physics 15 (2024) 131–57 [doi:10.1146/annurev-conmatphys-040423-014045, arXiv:2210.02530]
-
Pieralberto Marchetti: Introduction to abelian anyons in planar systems [arXiv;2507.03597]
On the history of the concept:
- Gerald A. Goldin: The Prediction of Anyons: Its History and Wider Implications, SciPost Phys. Proc. 14 005 (2023) [arXiv:2212.12632, doi: 10.21468/SciPostPhysProc.14.005]
Rigorous discussion in terms of superselection sectors in algebraic quantum field theory:
-
Jürg Fröhlich, Pieralberto Marchetti, Quantum field theory of anyons, Lett. Math. Phys. 16 (1988) 347–358 (reprinted in Wilczek 1990, p. 202-213) [doi:10.1007/BF00402043]
-
Jürg Fröhlich, Fabrizio Gabbiani, Braid statistics in local quantum theory, Reviews in Mathematical Physics, 2 03 (1990) 251-353 [doi:10.1142/S0129055X90000107]
-
Jürg Fröhlich, Fabrizio Gabbiani, Pieralberto Marchetti, Braid statistics in three-dimensional local quantum field theory, in: H.C. Lee (ed.) Physics, Geometry and Topology NATO ASI Series, 238 Springer (1990) [doi:10.1007/978-1-4615-3802-8_2, pdf]
-
Klaus Fredenhagen, Karl-Henning Rehren, Bert Schroer, Superselection sectors with braid group statistics and exchange algebras – I: General theory, Comm. Math. Phys. Volume 125, Number 2 (1989), 201-226. (euclid:cmp/1104179464)
-
Klaus Fredenhagen, Karl-Henning Rehren, Bert Schroer, Superselection sectors with braid group statistics and exchange algebras – II: Geometric aspects and conformal covariance, Reviews in Mathematical PhysicsVol. 04, No. spec01, pp. 113-157 (1992) (doi:10.1142/S0129055X92000170 pdf)
Discussion of anyon-wavefunctions as multi-valued functions on a configuration space of points:
-
Yong-Shi Wu, Multiparticle Quantum Mechanics Obeying Fractional Statistics, Phys. Rev. Lett. 53 (1984) 111 [doi:10.1103/PhysRevLett.53.111, pdf]
-
Tom Imbo, Chandni Shah Imbo, E. C. G. Sudarshan, Identical particles, exotic statistics and braid groups, Physics Letters B 234 1–2, (1990) 103-107 [doi:10.1016/0370-2693(90)92010-G, pdf]
-
Garth A. Baker, Geoff S. Canright, Shashikant B. Mulay, Carl Sundberg, On the spectral problem for anyons, Communications in Mathematical Physics 153 (1993) 277–295 [doi:10.1007/BF02096644]
-
J. Mund, Robert Schrader, Hilbert Spaces for Nonrelativistic and Relativistic “Free” Plektons (Particles with Braid Group Statistics), in Advances in dynamical systems and quantum physics (Capri, 1993), World Sci. (1995) 235–259 [arXiv:hep-th/9310054]
followed up by:
Klaus Fredenhagen, Matthias Gaberdiel and Stefan M. Rüger, Scattering states of plektons (particles with braid group statistics) in 2+1 dimensional quantum field theory, Communications in Mathematical Physics 175 (1996) 319–335 [doi:10.1007/BF02102411]
-
Gianfausto Dell’Antonio, Rodolfo Figari, Alessandro Teta: Statistics in Space Dimension Two, Letters in Mathematical Physics 40 (1997) 235–256 [doi:10.1023/A:1007361832622]
-
Jan Myrheim, Anyons, p. 265-414 in: Topological aspects of low dimensional systems, Les Houches LXIX, Springer (1999) [doi:10.1007/3-540-46637-1, pdf]
-
M.V.N. Murthy, Ramamurti Shankar, Exclusion Statistics: From Pauli to Haldane (1999, 2009) [dspace:123456789/334, pdf, pdf]
-
G. Date, M.V.N. Murthy, Radhika Vathsan, Classical and Quantum Mechanics of Anyons [arXiv:cond-mat/0302019]
The topic of quantum measurement of non-abelian anyons is crucial to their identification in experiment but has received little attenion, exceptions being:
-
Parsa Bonderson, Kirill Shtengel, Joost Slingerland, Decoherence of Anyonic Charge in Interferometry Measurements, Phys. Rev. Lett. 98 (2007) 070401 [doi:10.1103/PhysRevLett.98.070401, arXiv:quant-ph/0608119]
-
Parsa Bonderson, Kirill Shtengel, Joost Slingerland, Interferometry of non-Abelian Anyons, Annals Phys. 323 (2008) 2709-2755 [doi:10.1016/j.aop.2008.01.012, arXiv:0707.4206]
-
Andrey Morozov, On measuring the topological charge of anyons [arXiv:2403.07847]
Anyonic topological order in terms of braided fusion categories
Claim and status
In condensed matter theory it is folklore that species of anyonic topological order correspond to braided unitary fusion categories/modular tensor categories.
The origin of the claim is:
- Alexei Kitaev, Section 8 and Appendix E of: Anyons in an exactly solved model and beyond, Annals of Physics 321 1 (2006) 2-111 [doi:10.1016/j.aop.2005.10.005]
Early accounts re-stating this claim (without attribution):
-
Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, Sankar Das Sarma, pp. 28 of: Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80 1083 (2008) [doi:10.1103/RevModPhys.80.1083, arXiv:0707.1888]
-
Zhenghan Wang, Section 6.3 of: Topological Quantum Computation, CBMS Regional Conference Series in Mathematics 112, AMS (2010) [ISBN-13: 978-0-8218-4930-9]
Further discussion (mostly review and mostly without attribution):
-
Simon Burton, A Short Guide to Anyons and Modular Functors [arXiv:1610.05384]
(this one stands out as still attributing the claim to Kitaev (2006), Appendix E)
-
Eric C. Rowell, Zhenghan Wang, Mathematics of Topological Quantum Computing, Bull. Amer. Math. Soc. 55 (2018), 183-238 (arXiv:1705.06206, doi:10.1090/bull/1605)
-
Tian Lan, A Classification of (2+1)D Topological Phases with Symmetries [arXiv:1801.01210]
-
K. Beer et al.: From categories to anyons: a travelogue [arXiv:1811.06670]
-
Colleen Delaney, A categorical perspective on symmetry, topological order, and quantum information (2019) [uc:5z384290>, pdf]
-
Colleen Delaney, Lecture notes on modular tensor categories and braid group representations (2019) [pdf, pdf]
-
Liang Wang, Zhenghan Wang, In and around Abelian anyon models, J. Phys. A: Math. Theor. 53 505203 (2020) [doi:10.1088/1751-8121/abc6c0]
-
Parsa Bonderson, Measuring Topological Order, Phys. Rev. Research 3, 033110 (2021) [doi:10.1103/PhysRevResearch.3.033110, arXiv:2102.05677]
-
Zhuan Li, Roger S.K. Mong, Detecting topological order from modular transformations of ground states on the torus [arXiv:2203.04329]
-
Liang Kong, Zhi-Hao Zhang: An invitation to topological orders and category theory [arXiv:2205.05565]
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing [arXiv:2208.11762]
-
Sachin Valera, A Quick Introduction to the Algebraic Theory of Anyons, talk at CQTS Initial Researcher Meeting (Sep 2022) pdf]
-
Willie Aboumrad, Quantum computing with anyons: an F-matrix and braid calculator [arXiv:2212.00831]
-
Steven H. Simon, Topological Quantum, Oxford University Press (2023) [ISBN:9780198886723, pdf, webpage]
-
Siu-Hung Ng, Eric C. Rowell, Xiao-Gang Wen: Classification of modular data up to rank 12 [arXiv:2308.09670]
Emphasis that the expected description of anyons by braided fusion categories had remained folklore, together with a list of minimal assumptions that would need to be shown:
- Sachin J. Valera, Fusion Structure from Exchange Symmetry in (2+1)-Dimensions, Annals of Physics 429 (2021) [doi:10.1016/j.aop.2021.168471, arXiv:2004.06282]
An argument that the statement at least for SU(2)-anyons does follow from an enhancement of the K-theory classification of topological phases of matter to interacting topological order:
- Hisham Sati, Urs Schreiber, Anyonic topological order in TED K-theory, Rev. Math. Phys. 35 03 (2023) 2350001 [doi:10.1142/S0129055X23500010, arXiv:2206.13563]
In string/M-theory
Arguments realizing such anyonic topological order in the worldvolume-field theory on M5-branes:
Via KK-compactification on closed 3-manifolds (Seifert manifolds) analogous to the 3d-3d correspondence (which instead uses hyperbolic 3-manifolds):
-
Gil Young Cho, Dongmin Gang, Hee-Cheol Kim: M-theoretic Genesis of Topological Phases, J. High Energ. Phys. 2020 115 (2020) [arXiv:2007.01532, doi:10.1007/JHEP11(2020)115]
-
Shawn X. Cui, Paul Gustafson, Yang Qiu, Qing Zhang, From Torus Bundles to Particle-Hole Equivariantization, Lett Math Phys 112 15 (2022) [doi:10.1007/s11005-022-01508-3, arXiv:2106.01959]
-
Shawn X. Cui, Yang Qiu, Zhenghan Wang, From Three Dimensional Manifolds to Modular Tensor Categories, Commun. Math. Phys. 397 (2023) 1191–1235 [doi:10.1007/s00220-022-04517-4, arXiv:2101.01674]
-
Sunjin Choi, Dongmin Gang, Hee-Cheol Kim: Infrared phases of 3D Class R theories, J. High Energ. Phys. 2022 151 (2022) [doi:10.1007/JHEP11(2022)151, arXiv:2206.11982]
-
Federico Bonetti, Sakura Schäfer-Nameki, Jingxiang Wu, : 3d Topological Order Labeled by Seifert Manifolds [arXiv:2403.03973]
-
Hisham Sati, Urs Schreiber: Anyons on M5-Probes of Seifert 3-Orbifolds [arXiv:2411.16852]
-
Hisham Sati, Urs Schreiber: Engineering of Anyons on M5-Probes via Flux-Quantization [arXiv:2501.17927]
- Hisham Sati, Urs Schreiber: Anyonic Defect Branes and Conformal Blocks in Twisted Equivariant Differential K-Theory, Reviews in Mathematical Physics 35 06 (2023) 2350009 [arXiv:2203.11838, doi:10.1142/S0129055X23500095]
Further discussion
Relation to ZX-calculus:
- Fatimah Rita Ahmadi, Aleks Kissinger, Topological Quantum Computation Through the Lens of Categorical Quantum Mechanics [arXiv:2211.03855]
On detection of topological order by observing modular transformations on the ground state:
- Zhuan Li, Roger S. K. Mong, Detecting topological order from modular transformations of ground states on the torus, Phys. Rev. B 106 (2022) 235115 [doi:10.1103/PhysRevB.106.235115 arXiv:2203.04329]
See also:
- Liang Kong, Topological Wick Rotation and Holographic Dualities, talk at CQTS (Oct 2022) pdf]
Anyons in fractional quantum Hall systems
References on anyon-excitations (satisfying braid group statistics) in the quantum Hall effect (for more on the application to topological quantum computation see the references there):
The prediction of abelian anyon-excitations in the quantum Hall effect (i.e. satisfying braid group statistics in 1-dimensional linear representations of the braid group) by computation of Berry phases of Laughlin wavefunctions via the quantum adiabatic theorem:
-
Bertrand I. Halperin: Statistics of Quasiparticles and the Hierarchy of Fractional Quantized Hall States, Phys. Rev. Lett. 52 (1984) 1583 [doi:10.1103/PhysRevLett.52.1583]
Erratum, Phys. Rev. Lett. 52 (1984) 2390 [doi:10.1103/PhysRevLett.52.2390.4]
-
Daniel P. Arovas, John Robert Schrieffer, Frank Wilczek, Fractional Statistics and the Quantum Hall Effect, Phys. Rev. Lett. 53 (1984) 722 [doi:10.1103/PhysRevLett.53.722]
(for filling fraction )
-
W. P. Su: Statistics of the fractionally charged excitations in the quantum Hall effect, Phys. Rev. B 34 (1986) 1031 [doi:10.1103/PhysRevB.34.1031]
(claim for general filling fraction )
-
A. S. Goldhaber, Jainendra K. Jain: Characterization of fractional-quantum-Hall-effect quasiparticles, Physics Letters A 199 3–4 (1995) 267-273 [doi:10.1016/0375-9601(95)00101-8, arXiv:cond-mat/9501080]
(for Jain series fractions )
-
(review)
The original discussion of non-abelian anyon-excitations in the quantum Hall effect (i.e. satisfying braid group statistics in higher dimensional linear representations of the braid group, related to modular tensor categories):
- Gregory Moore, Nicholas Read, Nonabelions in the fractional quantum Hall effect, Nucl. Phys. 360B(1991)362 (pdf, doi:10.1016/0550-3213(91)90407-O)
Review:
-
Ady Stern, Anyons and the quantum Hall effect – A pedagogical review, Annals of Physics 323 1 (2008) 204-249 [doi:10.1016/j.aop.2007.10.008, arXiv:0711.4697]
-
Menelaos Zikidis: Abelian Anyons and Fractional Quantum Hall Effect, Seminar notes (2017) [pdf, pdf]
-
Ady Stern: Engineering Non-Abelian Quasi-Particles in Fractional Quantum Hall States – A Pedagogical Introduction, Ch. 9 in: Fractional Quantum Hall Effects, World Scientific (2020) 435-486 [doi:10.1142/9789811217494_0009]
-
D. E. Feldman, Bertrand Halperin: Fractional charge and fractional statistics in the quantum Hall effects, Rep. Prog. Phys. 84 (2021) 076501 [doi:10.1088/1361-6633/ac03aa, arXiv:2102.08998]
On (anyons in) fractional quantum Hall systems as potential quantum hardware for topological quantum computing:
-
D. V. Averin, V. J. Goldman: Quantum computation with quasiparticles of the fractional quantum Hall effect, Solid State Communications 121 1 (2001) 25-28 [doi:10.1016/S0038-1098(01)00447-1, arXiv:cond-mat/0110193]
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak: Topologically-Protected Qubits from a Possible Non-Abelian Fractional Quantum Hall State, Phys. Rev. Lett. 94 166802 (2005) [doi:10.1103/PhysRevLett.94.166802, arXiv:cond-mat/0412343]
-
Sergey Bravyi: Universal Quantum Computation with the Fractional Quantum Hall State, Phys. Rev. A 73 042313 (2006) [doi:10.1103/PhysRevA.73.042313, arXiv:quant-ph/0511178]
-
Maissam Barkeshli, Xiao-Liang Qi: Synthetic Topological Qubits in Conventional Bilayer Quantum Hall Systems, Phys. Rev. X 4 (2014) 041035 [doi:10.1103/PhysRevX.4.041035, arXiv:1302.2673]
-
Roger S. K. Mong et al.: Universal Topological Quantum Computation from a Superconductor-Abelian Quantum Hall Heterostructure, Phys. Rev. X 4 (2014) 011036 [doi:10.1103/PhysRevX.4.011036, arXiv:1307.4403]
Observation of anyons in fractional quantum Hall systems
While the occurrence of anyon-excitations in the fractional quantum Hall effect is a robust theoretical prediction (see the references above), and while the fractional quantum Hall effect itself has long been established in experiment, the actual observation of anyons in these systems is subtle.
An early claim of the observation of non-abelian anyons seems to remain unconfirmed:
- Sanghun An, P. Jiang, H. Choi, W. Kang, S. H. Simon, L. N. Pfeiffer, K. W. West, K. W. Baldwin, Braiding of Abelian and Non-Abelian Anyons in the Fractional Quantum Hall Effect [arXiv:1112.3400]
Observation in gallium arsenide () semiconductor heterostructures:
-
H. Bartolomei, et al.: Fractional statistics in anyon collisions, Science 368 6487 (2020) 173-177 [doi:10.1126/science.aaz5601, arXiv:2006.13157]
-
James Nakamura et al.: Aharonov–Bohm interference of fractional quantum Hall edge modes, Nature Physics 15 563–569 (2019) [doi:10.1038/s41567-019-0441-8, arXiv:1901.08452]
-
James Nakamura et al.: Direct observation of anyonic braiding statistics, Nat. Phys. 16 (2020) 931–936 [doi:10.1038/s41567-020-1019-1, arXiv:2006.14115]
-
Bob Yirka, Best evidence yet for existence of anyons, PhysOrg News (July 10, 2020) [phys.org/news/2020-07]
-
Davide Castelvecchi: Welcome anyons! Physicists find best evidence yet for long-sought 2D structures, Nature News, 583 (03 July 2020) 176-177 [doi:10.1038/d41586-020-01988-0]
-
James Nakamura et al.: Impact of bulk-edge coupling on observation of anyonic braiding statistics in quantum Hall interferometers, Nature Communications 13 344 (2022) [doi:10.1038/s41467-022-27958-w, arXiv:2107.02136]
-
James Nakamura et al.: Fabry-Perot interferometry at the fractional quantum Hall state, Phys. Rev. X 13 (2023) 041012 [doi:10.1103/PhysRevX.13.041012, arXiv:2304.12415]
-
M. Ruelle et al.: Comparing fractional quantum Hall Laughlin and Jain topological orders with the anyon collider, Physical Review X 13 (2023) 011031 [doi:10.1103/PhysRevX.13.011031, arXiv:2210.01066]
-
Pierre Glidic et al: Cross-Correlation Investigation of Anyon Statistics in the and Fractional Quantum Hall States, Phys. Rev. X 13 011030 (2023) [doi:10.1103/PhysRevX.13.011030, arXiv:2210.01054]
-
Pierre Glidic et al.: Signature of anyonic statistics in the integer quantum Hall regime, Nature Commun. 15 6578 (2024) 1 [doi:10.1038/s41467-024-50820-0, arXiv:2401.06069]
-
Hemanta Kumar Kundu et al.: Anyonic interference and braiding phase in a Mach-Zehnder interferometer, Nature Physics 19 (2023) 515–521 [doi:10.1038/s41567-022-01899-z, arXiv:2203.0420]
-
A. Veillon et al.: Observation of the scaling dimension of fractional quantum Hall anyons, Nature 632 (2024) 517–521 [doi:10.1038/s41586-024-07727-z]
-
Bikash Ghosh, Maria Labendik, Liliia Musina, Vladimir Umansky, Moty Heiblum, David F. Mross: Anyonic Braiding in a Chiral Mach-Zehnder Interferometer, Nature Physics (2025) [doi:10.1038/s41567-025-02960-3, arXiv:2410.16488]
and in graphene heterostructures:
-
Noah Samuelson et al.: Anyonic statistics and slow quasiparticle dynamics in a graphene fractional quantum Hall interferometer [arXiv:2403.19628]
-
Jehyun Kim et al.: Aharonov-Bohm Interference in Even-Denominator Fractional Quantum Hall States [arXiv:2412.19886]
See also:
- Flavio Ronetti et al.: Probing anyon statistics on a single-edge loop in the fractional quantum Hall regime [arXiv:2506.09774]
On appatent bound states of FQH anyons:
- Mytraya Gattu, Jainendra K. Jain: Molecular anyons in fractional quantum Hall effect [arXiv:2505.22782]
Superconducting defect anyons in FQH systems
On non-abelian (parafermionic Majorana zero mode) defect anyons associated with superconducting islands inside abelian fractional quantum Hall systems:
-
Netanel H. Lindner, Erez Berg, Gil Refael, Ady Stern: Fractionalizing Majorana fermions: non-abelian statistics on the edges of abelian quantum Hall states, Phys. Rev. X 2 (2012) 041002 [doi:10.1103/PhysRevX.2.041002arXiv:1204.5733]
-
David J. Clarke, Jason Alicea, Kirill Shtengel: Exotic non-Abelian anyons from conventional fractional quantum Hall states, Nature Communications 4 1348 (2013) [ncomms:2340, arXiv:1204.5479]
-
Abolhassan Vaezi: Fractional topological superconductor with fractionalized Majorana fermions, Phys. Rev. B 87 (2013) 035132 [doi:10.1103/PhysRevB.87.035132, arXiv:1204.6245]
-
Roger S. K. Mong, David J. Clarke, Jason Alicea, Netanel H. Lindner, Paul Fendley, Chetan Nayak, Yuval Oreg, Ady Stern, Erez Berg, Kirill Shtengel, Matthew P. A. Fisher: Universal Topological Quantum Computation from a Superconductor-Abelian Quantum Hall Heterostructure, Phys. Rev. X 4 (2014) 011036 [doi:10.1103/PhysRevX.4.011036, arXiv:1307.4403]
-
Younghyun Kim, David J. Clarke, Roman M. Lutchyn: Coulomb Blockade in Fractional Topological Superconductors, Phys. Rev. B 96 (2017) 041123 [doi:10.1103/PhysRevB.96.041123, arXiv:1703.00498]
-
Luiz H. Santos, Taylor L. Hughes: Parafermionic Wires at the Interface of Chiral Topological States, Phys. Rev. Lett. 118 (2019) 136801 [doi:10.1103/PhysRevLett.118.136801]
-
Luiz H. Santos: Parafermions in Hierarchical Fractional Quantum Hall States, Phys. Rev. Research 2 (2020) 013232 [doi:10.1103/PhysRevResearch.2.013232, arXiv:1906.07188]
Anyons in topological superconductors
On anyon-excitations in topological superconductors.
via Majorana zero modes:
Original proposal:
- Nicholas Read, Dmitry Green, Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries, and the fractional quantum Hall effect, Phys. Rev. B61:10267, 2000 (arXiv:cond-mat/9906453)
Review:
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak, Majorana Zero Modes and Topological Quantum Computation, npj Quantum Information 1, 15001 (2015) (nature:npjqi20151)
-
Nur R. Ayukaryana, Mohammad H. Fauzi, Eddwi H. Hasdeo, The quest and hope of Majorana zero modes in topological superconductor for fault-tolerant quantum computing: an introductory overview (arXiv:2009.07764)
-
Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors [arXiv:2301.11614]
Further developments:
-
Meng Cheng, Victor Galitski, Sankar Das Sarma, Non-adiabatic Effects in the Braiding of Non-Abelian Anyons in Topological Superconductors, Phys. Rev. B 84, 104529 (2011) (arXiv:1106.2549)
-
Javad Shabani et al., Two-dimensional epitaxial superconductor-semiconductor heterostructures: A platform for topological superconducting networks, Phys. Rev. B 93 155402 (2016) [doi:10.1103/PhysRevB.93.155402, arXiv:1511.01127]
-
Javad Shabani et al., Zero-Energy Modes from Coalescing Andreev States in a Two-Dimensional Semiconductor-Superconductor Hybrid Platform, Phys. Rev. Lett. 119 (2017) 176805 [doi:10.1103/PhysRevLett.119.176805, arXiv:1703.03699]
-
Javad Shabani et al., Fusion of Majorana Bound States with Mini-Gate Control in Two-Dimensional Systems, Nature Communications 13 (2022) 1738-1747 [doi:10.1038/s41467-022-29463-6, arXiv:2101.09272]
-
Javad Shabani et al., Quasiparticle dynamics in epitaxial Al-InAs planar Josephson junctions, PRX Quantum 4 030339 (2023) [doi:10.1103/PRXQuantum.4.030339, arXiv:2303.04784]
-
William F. Schiela, Peng Yu, Javad Shabani: Progress in superconductor-semiconductor topological Josephson junctions, PRX Quantum 5 (2024) 030102 [doi:10.1103/PRXQuantum.5.030102, arXiv:2408.12749]
via Majorana zero modes restricted to edges of topological insulators:
- Biao Lian, Xiao-Qi Sun, Abolhassan Vaezi, Xiao-Liang Qi, Shou-Cheng Zhang: Topological quantum computation based on chiral Majorana fermions, PNA 115 43 (2018) 10938-10942 [doi:10.1073/pnas.1810003115]
Concerning measurement-based quantum gates on Majorana zero modes:
- Torsten Karzig, Yuval Oreg, Gil Refael, Michael H. Freedman: Robust Majorana magic gates via measurements, Phys. Rev. B 99 (2019) 144521 [doi:10.1103/PhysRevB.99.144521, arXiv:1812.10498]
See also:
- Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Anyons and Non-Abelian Vortices in Topological Superconductors arXiv:2301.11614
Defect anyons
Often the concept of anyons is introduced as if a generalization of particle statistics of perturbative quanta like fundamental bosons and fermions. But many (concepts of) types of anyons are really solitonicdefects such as vortices whose braiding phases are adiabatic Berry phases.
The general concept of braiding of defects in solid state physics:
- N. David Mermin, The topological theory of defects in ordered media, Rev. Mod. Phys. 51 (1979) 591 doi:10.1103/RevModPhys.51.591
(including a review of basic homotopy theory)
and more specifically for vortices:
- Hoi-Kwong Lo, John Preskill, Non-Abelian vortices and non-Abelian statistics, Phys. Rev. D 48 (1993) 4821 [doi:10.1103/PhysRevD.48.4821]
Explicit discussion as defect anyons:
- Alexei Kitaev, Anyons in an exactly solved model and beyond, Annals of Physics 321 1 (2006) 2-111 [doi:10.1016/j.aop.2005.10.005]
[p. 4:] “Anyonic particles are best viewed as a kind of topological defects that reveal nontrivial properties of the ground state.”
and with focus on defect anyons in momentum space:
- Hisham Sati, Urs Schreiber: Anyonic topological order in TED K-theory, Reviews in Mathematical Physics 35 03 (2023) 2350001 [doi:10.1142/S0129055X23500010, arXiv:2206.13563]
Anyonic defects which act as genons, changing the effective genus of the ambient 2D surface:
-
Maissam Barkeshli, Xiao-Liang Qi: Topological Nematic States and Non-Abelian Lattice Dislocations, Phys. Rev. X 2 031013 (2012) [doi:10.1103/PhysRevX.2.031013, arXiv:1112.3311]
-
Maissam Barkeshli, Chao-Ming Jian, Xiao-Liang Qi: Twist defects and projective non-Abelian braiding statistics, Phys. Rev. B 87 (2013) 045130 [doi:10.1103/PhysRevB.87.045130, arXiv:1208.4834]
-
Xiao-Liang Qi: Defects in topologically ordered states, talk notes (2014) [pdf, pdf]
-
Maissam Barkeshli, Michael Freedman: Modular transformations through sequences of topological charge projections, Phys. Rev. B 94 (2016) 165108 [doi:10.1103/PhysRevB.94.165108, arXiv:1602.01093]
and specifically in quantum Hall systems:
-
Maissam Barkeshli, Xiao-Liang Qi: Synthetic Topological Qubits in Conventional Bilayer Quantum Hall Systems, Phys. Rev. X 4 (2014) 041035 [doi:10.1103/PhysRevX.4.041035, arXiv:1302.2673]
-
Andrey Gromov: Geometric Defects in Quantum Hall States, Phys. Rev. B 94 085116 (2016) [doi:10.1103/PhysRevB.94.085116]
see also:
- Simon Burton, Elijah Durso-Sabina, Natalie C. Brown: Genons, Double Covers and Fault-tolerant Clifford Gates [arXiv:2406.09951]
and their potential experimental realization:
- Zhao Liu, Gunnar Möller, Emil J. Bergholtz: Exotic Non-Abelian Topological Defects in Lattice Fractional Quantum Hall States, Phys. Rev. Lett. 119 (2017) 106801 [doi:10.1103/PhysRevLett.119.106801]
Concrete vortexanyons in Bose-Einstein condensates:
-
B. Paredes, P. Fedichev, J. Ignacio Cirac, Peter Zoller: 1/2-Anyons in small atomic Bose-Einstein condensates, Phys. Rev. Lett. 87 (2001) 010402 [doi:10.1103/PhysRevLett.87.010402, arXiv:cond-mat/0103251]
-
Julien Garaud, Jin Dai, Antti J. Niemi, Vortex precession and exchange in a Bose-Einstein condensate, J. High Energ. Phys. 2021 157 (2021) [arXiv:2010.04549]
-
Thomas Mawson, Timothy Petersen, Joost Slingerland, Tapio Simula, Braiding and fusion of non-Abelian vortex anyons, Phys. Rev. Lett. 123 (2019) 140404 [doi:10.1103/PhysRevLett.123.140404]
and in (other) superfluids:
- Yusuke Masaki, Takeshi Mizushima, Muneto Nitta, Non-Abelian Half-Quantum Vortices in 3P2 Topological Superfluids [arXiv:2107.02448]
and in condensates of non-defect anyons:
- Michele Correggi, Romain Duboscq, Douglas Lundholm, Nicolas Rougerie: Vortex patterns in the almost-bosonic anyon gas, Europhys. Lett. 126 (2019) 20005 [doi:10.1209/0295-5075/126/20005, arXiv:1901.10739]
On analog behaviour in liquid crystals:
- Alexander Mietke, Jörn Dunkel: Anyonic defect braiding and spontaneous chiral symmetry breaking in dihedral liquid crystals, Phys. Rev. X 12 (2022) 011027 [arXiv:2011.04648, doi:10.1103/PhysRevX.12.011027]
See also Ahn, Park & Yang 19 who refer to the band nodes in the Brillouin torus of a semi-metal as “vortices in momentum space”.
And see at defect brane.
Anyons in momentum-space
On non-trivial braiding of nodal points in the Brillouin torus of topological semi-metals (“braiding in momentum space”):
-
Junyeong Ahn, Sungjoon Park, Bohm-Jung Yang, Failure of Nielsen-Ninomiya theorem and fragile topology in two-dimensional systems with space-time inversion symmetry: application to twisted bilayer graphene at magic angle, Phys. Rev. X 9 (2019) 021013 [doi:10.1103/PhysRevX.9.021013, arXiv:1808.05375]
“here are band crossing points, henceforth called vortices”
-
QuanSheng Wu, Alexey A. Soluyanov, Tomáš Bzdušek, Non-Abelian band topology in noninteracting metals, Science 365 (2019) 1273-1277 [doi:10.1126/science.aau8740, arXiv:1808.07469]
“fundamental group of complement of nodal points/lines considered above (3)”
-
Apoorv Tiwari, Tomáš Bzdušek, Non-Abelian topology of nodal-line rings in PT-symmetric systems, Phys. Rev. B 101 (2020) 195130 [doi:10.1103/PhysRevB.101.195130]
“a new type non-Abelian ‘braiding’ of nodal-line rings inside the momentum space”
-
Adrien Bouhon, QuanSheng Wu, Robert-Jan Slager, Hongming Weng, Oleg V. Yazyev, Tomáš Bzdušek, Non-Abelian reciprocal braiding of Weyl points and its manifestation in ZrTe, Nature Physics 16 (2020) 1137-1143 [doi:10.1038/s41567-020-0967-9, arXiv:1907.10611]
“Here we report that Weyl points in three-dimensional (3D) systems with symmetry carry non-Abelian topological charges. These charges are transformed via non-trivial phase factors that arise upon braiding the nodes inside the reciprocal momentum space.”
Braiding of Dirac points in twisted bilayer graphene:
-
Jian Kang, Oskar Vafek: Non-Abelian Dirac node braiding and near-degeneracy of correlated phases at odd integer filling in magic angle twisted bilayer graphene, Phys. Rev. B 102 (2020) 035161 [doi:10.1103/PhysRevB.102.035161, arXiv:2002.10360]
-
Bin Jiang, Adrien Bouhon, Zhi-Kang Lin, Xiaoxi Zhou, Bo Hou, Feng Li, Robert-Jan Slager, Jian-Hua Jiang: Experimental observation of non-Abelian topological acoustic semimetals and their phase transitions, Nature Physics 17 (2021) 1239-1246 [doi:10.1038/s41567-021-01340-x, arXiv:2104.13397]
(analog realization in phononic crystals)
Here, we consider an exotic type of topological phases beyond the above paradigms that, instead, depend on topological charge conversion processes when band nodes are braided with respect to each other in momentum space or recombined over the Brillouin zone. The braiding of band nodes is in some sense the reciprocal space analog of the non-Abelian braiding of particles in real space. […] we experimentally observe non-Abelian topological semimetals and their evolutions using acoustic Bloch bands in kagome acoustic metamaterials. By tuning the geometry of the metamaterials, we experimentally confirm the creation, annihilation, moving, merging and splitting of the topological band nodes in multiple bandgaps and the associated non-Abelian topological phase transitions
-
Haedong Park, Stephan Wong, Xiao Zhang, and Sang Soon Oh, Non-Abelian Charged Nodal Links in a Dielectric Photonic Crystal, ACS Photonics 8 (2021) 2746–2754 [doi:10.1021/acsphotonics.1c00876]
-
Siyu Chen, Adrien Bouhon, Robert-Jan Slager, Bartomeu Monserrat, Non-Abelian braiding of Weyl nodes via symmetry-constrained phase transitions (formerly: Manipulation and braiding of Weyl nodes using symmetry-constrained phase transitions), Phys. Rev. B 105 (2022) L081117 [doi:10.1103/PhysRevB.105.L081117, arXiv:2108.10330]
“Our work opens up routes to readily manipulate Weyl nodes using only slight external parameter changes, paving the way for the practical realization of reciprocal space braiding.”
-
Bo Peng, Adrien Bouhon, Robert-Jan Slager, Bartomeu Monserrat, Multi-gap topology and non-Abelian braiding of phonons from first principles, Phys. Rev. B 105 (2022) 085115 [arXiv:2111.05872, doi:10.1103/PhysRevB.105.085115]
(analog realization in phononic crystals)
new opportunities for exploring non-Abelian braiding of band crossing points (nodes) in reciprocal space, providing an alternative to the real space braiding exploited by other strategies.
Real space braiding is practically constrained to boundary states, which has made experimental observation and manipulation difficult; instead, reciprocal space braiding occurs in the bulk states of the band structures and we demonstrate in this work that this provides a straightforward platform for non-Abelian braiding.
-
Bo Peng, Adrien Bouhon, Bartomeu Monserrat, Robert-Jan Slager, Phonons as a platform for non-Abelian braiding and its manifestation in layered silicates, Nature Communications 13 423 (2022) [doi:10.1038/s41467-022-28046-9]
(analog realization in phononic crystals)
it is possible to controllably braid Kagome band nodes in monolayer using strain and/or an external electric field.
-
Haedong Park, Wenlong Gao, Xiao Zhang, Sang Soon Oh, Nodal lines in momentum space: topological invariants and recent realizations in photonic and other systems, Nanophotonics 11 11 (2022) 2779–2801 [doi:10.1515/nanoph-2021-0692]
(analog realization in photonic crystals)
-
Adrien Bouhon, Robert-Jan Slager, Multi-gap topological conversion of Euler class via band-node braiding: minimal models, PT-linked nodal rings, and chiral heirs [arXiv:2203.16741]
See also:
-
Robert-Jan Slager, Adrien Bouhon, Fatma Nur Ünal, Floquet multi-gap topology: Non-Abelian braiding and anomalous Dirac string phase, Nature Communications 15 1144 (2024) [arXiv:2208.12824, doi:10.1038/s41467-024-45302-2]
-
Huahui Qiu et al., Minimal non-abelian nodal braiding in ideal metamaterials, Nature Communications 14 1261 (2023) [doi:10.1038/s41467-023-36952-9]
-
Wojciech J. Jankowski, Mohammedreza Noormandipour, Adrien Bouhon, Robert-Jan Slager: Disorder-induced topological quantum phase transitions in Euler semimetals, Phys. Rev. B 110 (2024) 064202 [arXiv:2306.13084, doi:10.1103/PhysRevB.110.064202]
-
Seung Hun Lee, Yuting Qian, Bohm-Jung Yang, Euler band topology in spin-orbit coupled magnetic systems [arXiv:2404.16383]
“Based on first-principles calculations, we report that such nodal point braiding in 2D electronic bands can be realized in a MSWI candidate, the bilayer with in-plane ferromagnetism under pressure. […] one can expect that the braiding of nodes can be achieved in 2D bilayer under the influence of an external in-plane Zeeman field.”
Incidentally, references indicating that the required toroidal (or yet higher genus) geometry for anyonic topological order in position space is dubious (as opposed to the evident toroidal geometry of the momentum-space Brillouin torus): Lan 19, p. 1, ….
Exposition:
-
Gunnar F. Lange: Multi-gap topology & non-abelian braiding in -space, talk at University of Oslo (Feb 2023) pdf]
-
Adrien Bouhon: Non-Abelian and Euler multi-gap topologies in crystalline materials, talk at: Quantum Information and Quantum Matter, CQTS @ NYU Abu Dhabi (May 2023) pdf]
Knotted nodal lines in 3d semimetals
Beware that various authors consider braids/knots formed by nodal lines in 3d semimetals, i.e. knotted nodal lines in 3 spatial dimensions, as opposed to worldlines (in 2+1 spacetime dimensions) of nodal points in effectively 2d semimetals needed for the anyon-braiding considered above.
An argument that these nodal lines in 3d space, nevertheless, may be controlled by Chern-Simons theory:
- Biao Lian, Cumrun Vafa, Farzan Vafa, Shou-Cheng Zhang, Chern-Simons theory and Wilson loops in the Brillouin zone, Phys. Rev. B 95 (2017) 094512 [doi:10.1103/PhysRevB.95.094512]
Topological quantum computation with anyons
The idea of topological quantum computation via a Chern-Simons theory with anyon braiding defects is due to:
-
Alexei Kitaev, Fault-tolerant quantum computation by anyons, Annals Phys. 303 (2003) 2-30 [doi:10.1016/S0003-4916(02)00018-0, arXiv:quant-ph/9707021]
-
Michael Freedman, P/NP, and the quantum field computer, Proc. Nat. Acad. Sci. 95 1 (1998) 98-101 [doi:10.1073/pnas.95.1.9]
-
Michael Freedman, Alexei Kitaev, Michael Larsen, Zhenghan Wang, Topological quantum computation, Bull. Amer. Math. Soc. 40 (2003), 31-38 [doi:10.1090/S0273-0979-02-00964-3, arXiv:quant-ph/0101025, pdf]
-
Michael Freedman, Michael Larsen, Zhenghan Wang, A modular functor which is universal for quantum computation, Communications in Mathematical Physics. 227 3 (2002) 605-622 [doi:10.1007/s002200200645, arXiv:quant-ph/0001108]
(specifically via su(2)-anyons)
-
Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, Sankar Das Sarma, Non-Abelian Anyons and Topological Quantum Computation, Rev. Mod. Phys. 80 1083 (2008) [doi:10.1103/RevModPhys.80.1083, arXiv:0707.1888]
-
Dmitry Melnikov, Andrei Mironov, Sergey Mironov, Alexei Morozov, Andrey Morozov: Towards topological quantum computer, Nucl. Phys. B926 (2018) 491-508 [doi:10.1016/j.nuclphysb.2017.11.016, arXiv:1703.00431]
(via R-matrix-solutions to the quantum Yang-Baxter equation)
and via a Dijkgraaf-Witten theory (like Chern-Simons theory but with discrete gauge group):
-
R. Walter Ogburn, John Preskill, Topological Quantum Computation, in: Quantum Computing and Quantum Communications, Lecture Notes in Computer Science 1509, Springer (1998) [doi:10.1007/3-540-49208-9_31]
-
Carlos Mochon, Anyons from non-solvable finite groups are sufficient for universal quantum computation, Phys. Rev. A 67 022315 (2003) [doi:10.1103/PhysRevA.67.022315, arXiv:quant-ph/0206128]
-
Carlos Mochon, Anyon computers with smaller groups, Phys. Rev. A 69 032306 (2004) [doi:10.1103/PhysRevA.69.032306, arXiv:quant-ph/0306063]
Proposals more specifically for topological quantum gates implemented in fractional quantum Hall systems:
-
D. V. Averin, V.J. Goldman: Quantum computation with quasiparticles of the fractional quantum Hall effect, Solid State Communications 121 1 (2001) 25-28 [doi:10.1016/S0038-1098(01)00447-1, arXiv:cond-mat/0110193]
-
Sankar Das Sarma, Michael Freedman, Chetan Nayak: Topologically-Protected Qubits from a Possible Non-Abelian Fractional Quantum Hall State, Phys. Rev. Lett. 94 166802 (2005) [doi:10.1103/PhysRevLett.94.166802, arXiv:cond-mat/0412343]
-
Sergey Bravyi: Universal Quantum Computation with the Fractional Quantum Hall State, Phys. Rev. A 73 042313 (2006) [doi:10.1103/PhysRevA.73.042313, arXiv:quant-ph/0511178]
Monographs:
-
Zhenghan Wang, Topological Quantum Computation, CBMS Regional Conference Series in Mathematics 112, AMS 2010 (ISBN-13: 978-0-8218-4930-9, pdf)
-
Jiannis K. Pachos, Introduction to Topological Quantum Computation, Cambridge University Press (2012) [doi:10.1017/CBO9780511792908]
-
Tudor D. Stanescu, Part IV of: Introduction to Topological Quantum Matter & Quantum Computation, CRC Press 2020 (ISBN:9780367574116)
-
Steven H. Simon, Topological Quantum, Oxford University Press (2023) [ISBN:9780198886723, pdf, webpage]
Review:
-
Louis Kauffman, Quantum Topology and Quantum Computing, in: Samuel J. Lomonaco (ed.), Quantum Computation: A Grand Mathematical Challenge for the Twenty-First Century and the Millennium, Proceedings of Symposia in Applied Mathematics 58, AMS (2002) [pdf, doi:10.1090/psapm/058]
(in relation to quantum topology)
-
John Preskill: Topological Quantum Computation, Chapter 9 in: Quantum Computation, lecture notes (since 2004) [pdf, pdf]
-
Gavin K. Brennen, Jiannis K. Pachos, Why should anyone care about computing with anyons?, Proc. R. Soc. A 464 (2008) 1-24 [doi:10.1098/rspa.2007.0026, arXiv:0704.2241]
-
Ady Stern, Netanel H. Lindner: Topological Quantum Computation – From Basic Concepts to First Experiments, Science 339 6124 (2013) 1179-1184 [doi:10.1126/science.1231473, spire:2748124]
-
Eric C. Rowell, An Invitation to the Mathematics of Topological Quantum Computation, J. Phys.: Conf. Ser. 698 (2016) 012012 [doi:10.1088/1742-6596/698/1/012012, arXiv:1601.05288]
-
Ananda Roy, David P. DiVincenzo, Topological Quantum Computing, Lecture notes of the 48th IFF Spring School (2017) [arXiv:1701.05052]
-
Ville Lahtinen, Jiannis K. Pachos, A Short Introduction to Topological Quantum Computation, SciPost Phys. 3 021 (2017) [doi: 10.21468/SciPostPhys.3.3.021, arXiv:1705.04103]
-
Eric C. Rowell, Zhenghan Wang, Mathematics of Topological Quantum Computing, Bull. Amer. Math. Soc. 55 (2018), 183-238 (arXiv:1705.06206, doi:10.1090/bull/1605)
-
Bernard Field, Tapio Simula, Introduction to topological quantum computation with non-Abelian anyons, Quantum Science and Technology 3 (2018) 045004 [doi:10.1088/2058-9565/aacad2, arXiv:1802.06176]
-
Muhammad Ilyas, Quantum Field Theories, Topological Materials, and Topological Quantum Computing [arXiv:2208.09707]
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing [arXiv:2208.11762, spire:2141848]
-
Fabian Hassler: Topological quantum computing [arXiv:2410.13547]
-
Hisham Sati, Sachin Valera: Topological Quantum Computing, Encyclopedia of Mathematical Physics 2nd ed 4 (2025) 325-345 [doi:10.1016/B978-0-323-95703-8.00262-7]
-
Jason Alicea: What does it mean to create a topological qubit?, Quantum Frontiers blog (March 2025) [webpage]
Focus on abelian anyons:
-
Jiannis K. Pachos, Quantum computation with abelian anyons on the honeycomb lattice, International Journal of Quantum Information 4 6 (2006) 947-954 [doi:10.1142/S0219749906002328, arXiv:quant-ph/0511273]
-
James Robin Wootton, Dissecting Topological Quantum Computation, PhD thesis, Leeds (2010) [ethesis:1163, pdf, pdf]
“non-Abelian anyons are usually assumed to be better suited to the task. Here we challenge this view, demonstrating that Abelian anyon models have as much potential as some simple non-Abelian models. […] Though universal non-Abelian models are admittedly the holy grail of topological quantum computation, and rightly so, this thesis has shown that Abelian models are just as useful as non-universal non-Abelian models. […] Abelian models are a computationally powerful, fault-tolerant and experimentally realistic prospect for quantum computation.”
-
Seth Lloyd, Quantum computation with abelian anyons, Quantum Information Processing 1 1/2 (2002) [doi:10.1023/A:1019649101654, arXiv:quant-ph/0004010]
-
James R. Wootton, Jiannis K. Pachos: Universal Quantum Computation with Abelian Anyon Models, Electronic Notes in Theoretical Computer Science 270 2 (2011) 209-218 [doi:10.1016/j.entcs.2011.01.032, arXiv:0904.4373]
see also:
-
Menelaos Zikidis: Abelian Anyons and Fractional Quantum Hall Effect, Seminar notes (2017) [pdf, pdf]
-
Wade Bloomquist, Zhenghan Wang: On Topological Quantum Computing With Mapping Class Group Representations, J. Phys. A: Math. Theor. 52 (2019) 015301 [doi:10.1088/1751-8121/aaeea1, arXiv:1805.04622]
-
Yichen Hu, Biao Lian: Chiral Sachdev-Ye model: Integrability and chaos of anyons in , Phys. Rev. B 105 (2022) 125109 [doi:10.1103/PhysRevB.105.125109]
Realization in experiment (so far via quantum simulation of anyons on non-topological quantum hardware, cf. FF24, Fig 5, as in “topological codes” for quantum error correction):
on superconducting qbits:
- T. Andersen et al.: Non-Abelian braiding of graph vertices in a superconducting processor, Nature 618 (2023) 264–269 [arXiv:2210.10255, doi:10.1038/s41586-023-05954-4]
on trapped-ion quantum hardware:
-
Daniel Nigg, Markus Mueller, Esteban A. Martinez, Philipp Schindler, Markus Hennrich, Thomas Monz, Miguel A. Martin-Delgado, Rainer Blatt: Experimental Quantum Computations on a Topologically Encoded Qubit, Science 18 Jul 2014: Vol. 345, Issue 6194, pp. 302-305 (arXiv:1403.5426, doi:10.1126/science.1253742)
-
Mohsin Iqbal, Nathanan Tantivasadakarn: Topological Order from Measurements and Feed-Forward on a Trapped Ion Quantum Computer, Nature Communications Physics 7 (2024) 205 [doi:10.1038/s42005-024-01698-3, arXiv:2302.01917]
-
Mohsin Iqbal, Nathanan Tantivasadakarn, R. Verresen et al., Figure 5 in : Non-Abelian topological order and anyons on a trapped-ion processor, Nature 626 (2024) 505–511 [doi:10.1038/s41586-023-06934-4]
Nature research briefing: Topological matter created on a quantum chip produces quasiparticles with computing power [doi:10.1038/d41586-023-04126-8]
-
Michael Foss-Feig, Guido Pagano, Andrew C. Potter, Norman Y. Yao: Progress in Trapped-Ion Quantum Simulation, Annual Reviews of Condensed Matter Physics (2024) [arXiv:2409.02990 doi:10.1146/annurev-conmatphys-032822-045619]
Discussion of anyon braid gates via homotopy type theory:
-
David Jaz Myers, Hisham Sati, Urs Schreiber: Topological Quantum Gates in Homotopy Type Theory, Comm. Math. Phys. 405 172 (2024) [arXiv:2303.02382, doi:10.1007/s00220-024-05020-8]
-
David Jaz Myers: Topological Quantum Gates, talk at Running HoTT 2024, CQTS@NYUAD (April 2024) [video:kt]
Braid group representations (as topological quantum gates)
On linear representations of braid groups (see also at braid group statistics and interpretation as quantum gates in topological quantum computation):
- Ivan Marin, On the representation theory of braid groups, Annales mathématiques Blaise Pascal, 20 2 (2013) 193-260 (arXiv:math/0502118, dml:275607)
Review:
-
Chen Ning Yang, M. L. Ge (eds.). Braid Group, Knot Theory and Statistical Mechanics, Advanced Series in Mathematical Physics 9, World Scientific (1991) doi:10.1142/0796
(focus on quantum Yang-Baxter equation)
-
Camilo Arias Abad: Introduction to representations of braid groups, Rev. colomb. mat. 49 1 (2015) [doi:10.15446/recolma.v49n1.54160, arXiv:1404.0724]
-
Toshitake Kohno, Introduction to representation theory of braid groups, Peking 2018 (pdf, pdf)
in relation to modular tensor categories:
- Colleen Delaney, Lecture notes on modular tensor categories and braid group representations, 2019 (pdf, pdf)
Braid representations from the monodromy of the Knizhnik-Zamolodchikov connection on bundles of conformal blocks over configuration spaces of points:
-
Ivan Todorov, Ludmil Hadjiivanov, Monodromy Representations of the Braid Group, Phys. Atom. Nucl. 64 (2001) 2059-2068; Yad.Fiz. 64 (2001) 2149-2158 arXiv:hep-th/0012099, doi:10.1134/1.1432899
-
Ivan Marin, Sur les représentations de Krammer génériques, Annales de l’Institut Fourier, 57 6 (2007) 1883-1925 numdam:AIF_2007__57_6_1883_0
and understood in terms of anyon statistics:
- Xia Gu, Babak Haghighat, Yihua Liu, Ising- and Fibonacci-Anyons from KZ-equations, J. High Energ. Phys. 2022 15 (2022) [doi:10.1007/JHEP09(2022)015, arXiv:2112.07195]
Braid representations seen inside the topological K-theory of the braid group‘s classifying space:
-
Alejandro Adem, Daniel C. Cohen, Frederick R. Cohen, On representations and K-theory of the braid groups, Math. Ann. 326 (2003) 515-542 (arXiv:math/0110138, doi:10.1007/s00208-003-0435-8)
-
Frederick R. Cohen, Section 3 of: On braid groups, homotopy groups, and modular forms, in: J.M. Bryden (ed.), Advances in Topological Quantum Field Theory, Kluwer 2004, 275–288 (pdf)
See also:
- R. B. Zhang, Braid group representations arising from quantum supergroups with arbitrary and link polynomials, Journal of Mathematical Physics 33, 3918 (1992) (doi:10.1063/1.529840)
As quantum gates for topological quantum computation with anyons:
-
Louis H. Kauffman, Samuel J. Lomonaco, Braiding Operators are Universal Quantum Gates, New Journal of Physics 6 (2004) [doi:10.1088/1367-2630/6/1/134, arXiv:quant-ph/0401090]
(via R-matrix solutions to the quantum Yang-Baxter equation)
-
Yong Zhang, Louis H. Kauffman, Mo-Lin Ge: Yang–Baxterizations, Universal Quantum Gates and Hamiltonians, Quantum Inf Process 4 (2005) 159–197 [doi:10.1007/s11128-005-7655-7]
(via R-matrix solutions to the quantum Yang-Baxter equation)
-
Samuel J. Lomonaco, Louis Kauffman, Topological Quantum Computing and the Jones Polynomial, Proc. SPIE 6244, Quantum Information and Computation IV, 62440Z (2006) (arXiv:quant-ph/0605004)
(braid group representation serving as a topological quantum gate to compute the Jones polynomial)
-
Louis H. Kauffman, Samuel J. Lomonaco, Topological quantum computing and braid group representations, Proceedings Volume 6976, Quantum Information and Computation VI; 69760M (2008) (doi:10.1117/12.778068, rg:228451452)
-
C.-L. Ho, A. I. Solomon, C.-H. Oh: Quantum entanglement, unitary braid representation and Temperley-Lieb algebra, EPL 92 (2010) 30002 [doi:10.1209/0295-5075/92/30002, arXiv:1011.6229]
-
Rebecca Chen: Generalized Yang-Baxter Equations and Braiding Quantum Gates, Journal of Knot Theory and Its Ramifications 21 09 (2012) 1250087 [arXiv:1108.5215, doi:10.1142/S0218216512500873]
-
Louis H. Kauffman, Majorana Fermions and Representations of the Braid Group, International Journal of Modern Physics A 33 23 (2018) 1830023 [doi:10.1142/S0217751X18300235, arXiv:1710.04650]
-
David Lovitz, Universal Braiding Quantum Gates [arXiv:2304.00710]
Introduction and review:
-
Colleen Delaney, Eric C. Rowell, Zhenghan Wang, Local unitary representations of the braid group and their applications to quantum computing, Revista Colombiana de Matemáticas(2017), 50 (2):211 (arXiv:1604.06429, doi:10.15446/recolma.v50n2.62211)
-
Eric C. Rowell, Braids, Motions and Topological Quantum Computing arXiv:2208.11762
Realization of Fibonacci anyons on quasicrystal-states:
- Marcelo Amaral, David Chester, Fang Fang, Klee Irwin, Exploiting Anyonic Behavior of Quasicrystals for Topological Quantum Computing, Symmetry 14 9 (2022) 1780 arXiv:2207.08928, doi:10.3390/sym14091780
Realization on supersymmetric spin chains:
- Indrajit Jana, Filippo Montorsi, Pramod Padmanabhan, Diego Trancanelli, Topological Quantum Computation on Supersymmetric Spin Chains arXiv:2209.03822
See also:
- Yuanjie Ren, Peter Shor, Topological quantum computation assisted by phase transitions [arXiv:2311.00103]
Compilation to braid gate circuits
On approximating (cf. the Solovay-Kitaev theorem) given quantum gates by (i.e. compiling them to) cicuits of anyon braid gates (generally considered for su(2)-anyons and here mostly for universal Fibonacci anyons, to some extent also for non-universal Majorana anyons):
-
Nicholas E. Bonesteel, Layla Hormozi, Georgios Zikos, Steven H. Simon, Braid Topologies for Quantum Computation, Phys. Rev. Lett. 95 140503 (2005) [doi:10.1103/PhysRevLett.95.140503, arXiv:quant-ph/0505065]
-
Layla Hormozi, Georgios Zikos, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Compiling, Phys. Rev. B 75 165310 (2007) [doi:10.1103/PhysRevB.75.165310, arXiv:quant-ph/0610111]
-
Layla Hormozi, Nicholas E. Bonesteel, Steven H. Simon, Topological Quantum Computing with Read-Rezayi States, Phys. Rev. Lett. 103 160501 (2009) [doi:10.1103/PhysRevLett.103.160501, arXiv:0903.2239]
-
M. Baraban, Nicholas E. Bonesteel, Steven H. Simon, Resources required for topological quantum factoring, Phys. Rev. A 81 062317 (2010) [doi:10.1103/PhysRevA.81.062317, arXiv:1002.0537]
(focus on compiling Shor's algorithm)
-
Vadym Kliuchnikov, Alex Bocharov, Krysta M. Svore, Asymptotically Optimal Topological Quantum Compiling, Phys. Rev. Lett. 112 140504 (2014) [doi:10.1103/PhysRevLett.112.140504, arXiv:1310.4150, talk recording: doi:10.48660/13100129]
-
Joren W. Brunekreef, Topological Quantum Computation and Quantum Compilation, Utrecht (2014) [hdl:20.500.12932/17738]
-
Yuan-Hang Zhang, Pei-Lin Zheng, Yi Zhang, Dong-Ling Deng, Topological Quantum Compiling with Reinforcement Learning, Phys. Rev. Lett. 125 170501 (2020) [doi:10.1103/PhysRevLett.125.170501, arXiv:2004.04743]
-
Emil Génetay-Johansen, Tapio Simula, Section IV of: Fibonacci anyons versus Majorana fermions – A Monte Carlo Approach to the Compilation of Braid Circuits in Anyon Models, PRX Quantum 2 010334 (2021) [doi:10.1103/PRXQuantum.2.010334, arXiv:2008.10790]
-
Cheng-Qian Xu, D. L. Zhou, Quantum teleportation using Ising anyons, Phys. Rev. A 106 012413 (2022) [doi:10.1103/PhysRevA.106.012413, arXiv:2201.11923]
(focus on implemening the quantum teleportation-protocol with Ising anyons)
Approximating all topological quantum gates by just the weaves among all braids:
-
Steven H. Simon, Nick E. Bonesteel, Michael H. Freedman, N. Petrovic, Layla Hormozi, Topological Quantum Computing with Only One Mobile Quasiparticle, Phys. Rev. Lett. 96 (2006) 070503 (arXiv:quant-ph/0509175, doi:10.1103/PhysRevLett.96.070503)
-
Layla Hormozi, Georgios Zikos, Nick E. Bonesteel, Steven H. Simon, Topological quantum compiling, Phys. Rev. B 75, 165310 (doi:10.1103/PhysRevB.75.165310, arXiv:quant-ph/0610111)
-
Mohamed Taha Rouabah, Compiling single-qubit braiding gate for Fibonacci anyons topological quantum computation (arXiv:2008.03542)
Last revised on August 21, 2025 at 08:50:40. See the history of this page for a list of all contributions to it.